Previously we claimed that if you want to check whether a category “behaves like a category of spaces,” you can try checking whether it’s distributive. The goal of today’s post is to justify the assertion that objects in distributive categories behave like spaces by showing that they have a notion of “connected components.”
For starters, let be a distributive category with terminal object
, and let
be the coproduct of two copies of
. For an object
, what does
look like? If
and
is a sufficiently well-behaved topological space, morphisms
correspond to subsets of the connected components of
, and
naturally has have the structure of a Boolean algebra or Boolean ring whose elements can be interpreted as subsets of the connected components of
.
It turns out that naturally has the structure of a Boolean algebra or Boolean ring (more invariantly, the structure of a model of the Lawvere theory of Boolean functions) in any distributive category. Hence any distributive category naturally admits a contravariant functor into Boolean rings, or, via Stone duality, a covariant functor into profinite sets / Stone spaces. This is our “connected components” functor. When
the object this functor outputs is known as the Pierce spectrum.
This construction can be thought of as trying to do for what the étale fundamental group does for
.
The proof
In general, in a category with finite products, the set
naturally acquires the structure of a model of the Lawvere theory generated by
, namely the full subcategory on the finite products
. (In our previous post on Lawvere theories we made use of the analogous construction for finite coproducts of
.)
How can we calculate this Lawvere theory when in a distributive category? Using distributivity! By induction, it’s not hard to see that
is literally the coproduct of
copies of
in any distributive category. It follows that a morphism
is a
-tuple of morphisms
. There are two distinguished such morphisms, namely the two coproduct inclusions into
, and using these two morphisms we can write down for any Boolean function a map
, in a way that agrees with products and composition.
(Edit: This section previously contained a mistake which was pointed out by Zhen Lin in the comments.)
More abstractly, if is any distributive category then there is a natural functor
given by sending a finite set
to the coproduct
, and by distributivity this functor preserves finite products in addition to finite coproducts. Above we’re looking at the image of the sets
and morphisms between them under this functor, which are the objects
and some distinguished morphisms between them.
(Note that distributivity can even be regarded as the crucial ingredient in the proof we outlined previously that Boolean functions can all be generated by constants and the if-then-else ternary operator; the key observation in that proof is that we can distribute , which is what let us express
-ary Boolean functions in terms of pairs of
-ary Boolean functions using if-then-else.)
It follows that in any distributive category, naturally acquires the structure of a model of the Lawvere theory of Boolean functions (so, according to taste, either a Boolean algebra or a Boolean ring).
The intuition
Intuitively, a morphism is a way to disconnect
into two pieces, namely the pullbacks
where the morphism
is either of the two coproduct inclusions, although
is probably not the coproduct of these two pieces unless we assume the stronger condition that the ambient category is extensive. These can in turn be thought of as subsets of the connected components of
, and the Boolean algebra / ring structure then comes from the usual logical operations on such subsets, e.g. intersection and union.
The example of affine schemes
The example of affine schemes is worth working through in detail. First, the terminal object in affine schemes is
, and so
is
. It’s enlightening to rewrite this using the isomorphism
which reveals that is the free commutative ring on an idempotent, and hence that morphisms
, for
a commutative ring, are naturally in bijection with idempotents in
. Idempotents are in turn in bijection with direct product decompositions
and so morphisms of affine schemes really do correspond to ways to disconnect
into pieces
. Abstractly, this reflects the fact that
is extensive, and not only distributive.
The abstract discussion above implies that the set of idempotents in canonically acquires the structure of a Boolean ring, which we’ll denote
. The multiplication in
is just the usual multiplication on idempotents, but the addition is the following modified addition
: if
are idempotents, then
.
Note that the third term disappears if has characteristic
. Geometrically we can think of
as indicator functions of unions of connected components of
; then the RHS describes the operation that must be performed on indicator functions, regarded as taking values in
, to get XOR.
Altogether, we find that taking idempotents gives a functor from commutative rings to Boolean rings. (Curiously, it is not the right adjoint to the inclusion of Boolean rings into commutative rings, although it does preserve limits.) Taking opposite categories, we get a functor from affine schemes to profinite sets called the Pierce spectrum functor, which we’ll denote
.
consists off a point iff
is connected, meaning it has exactly two idempotents,
and
(which are not equal, so the zero ring is not connected). This condition is equivalent to the Zariski spectrum
being connected as a topological space, and holds, for example, for any integral domain.
The Pierce spectrum organizes the Zariski spectrum into “connected components” as follows. If is a prime ideal of
, then the quotient map
induces a map
on Pierce spectra. Since the Pierce spectrum of is a point, we can associate to
a unique point in
, which intuitively is the connected component to which the point
belongs. This construction organizes into a natural map
where on the LHS denotes the prime spectrum as a topological space. (Curiously, this is a map on underlying topological spaces between two ringed spaces which cannot be promoted to a map of ringed spaces, basically because the natural inclusion of the Boolean ring object
into the affine line
is not a morphism of ring objects.)
The fibers of this map can be given natural affine scheme structures, as follows. An element of the Pierce spectrum can be thought of as a homomorphism
of Boolean rings. These can be regarded as generalizations of ultrafilters, which they reduce to in the special case that
is a product
of copies of
(so that the Pierce spectrum
is the Stone-Čech compactification
). This occurs whenever
is a product
of connected rings (e.g. integral domains).
Accordingly, there is a generalization of an ultraproduct construction we can perform here: given , we can quotient
by the ideal generated by the elements of
(which, recall, are idempotents in
). The result, which we’ll call
in deference to ultraproduct notation, is a connected ring, since every idempotent in
belongs to either
or
and hence gets identified with either
or
in this quotient, and in fact any morphism from
to a connected ring must factor through one of these morphisms
. Geometrically this says that any morphism from a connected affine scheme to
factors through some
, so these quotients really do deserve the name “connected components.”
Example. Let . On math.SE, Martin Brandenburg recently asked what one can say about the Zariski spectrum of
, and Eric Wofsey gave an excellent answer in terms of looking at the fibers of
over its Pierce spectrum exactly as above (which in fact motivated the writing of this post).
In this case is
, so the Pierce spectrum is
, which can be identified with the space of ultrafilters
on
, and the fibers are given by ultraproducts. These ultraproducts admit many interesting prime ideals: for example, if
is any sequence of primes, then we get a quotient map
to an ultraproduct of fields, which is again a field. So there is a prime ideal for every “nonstandard prime.”
[…] the data of such a decomposition is equivalent to the data of a continuous function from the Pierce spectrum to […]
[…] connected components of to with finite image, or equivalently to continuous functions from the Pierce spectrum to […]
Your claim that morphisms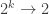 are the same as maps
are the same as maps 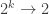 is not correct. Indeed, things go wrong already for
is not correct. Indeed, things go wrong already for 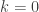 : consider sheaves on a disconnected space. Rather, what is true is that there is a unique (up to unique isomorphism) functor from the category of finite sets to any distributive category that preserves both finite products and finite coproducts. It may fail to be faithful (because the trivial category is distributive), and it may fail to be full.
: consider sheaves on a disconnected space. Rather, what is true is that there is a unique (up to unique isomorphism) functor from the category of finite sets to any distributive category that preserves both finite products and finite coproducts. It may fail to be faithful (because the trivial category is distributive), and it may fail to be full.
Regardless, because this functor preserves finite products, does always carry the structure of a boolean algebra in a distributive category. I don’t really know how to think of this. In an _extensive_ category, morphisms
does always carry the structure of a boolean algebra in a distributive category. I don’t really know how to think of this. In an _extensive_ category, morphisms 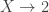 classify coproduct decompositions of
classify coproduct decompositions of  , so it makes some sense that there would be a connection with
, so it makes some sense that there would be a connection with  . The main examples of distributive categories you highlight – toposes, topological spaces, schemes – are actually extensive categories. So I wonder what happens in a distributive category that is not extensive?
. The main examples of distributive categories you highlight – toposes, topological spaces, schemes – are actually extensive categories. So I wonder what happens in a distributive category that is not extensive?
Ooh, I see where I went wrong. There can be interesting morphisms other than the coproduct inclusions… I’ll fix that. Thanks!
other than the coproduct inclusions… I’ll fix that. Thanks!
You’re right that the natural level of generality really seems to be extensive categories but I thought it was good to observe that this construction doesn’t require that additional hypothesis. I also haven’t thought much about extensive categories and I’m still in writing-short-posts mode because it’s November.