(Part I of this post is here)
Let denote the partition function, which describes the number of ways to write
as a sum of positive integers, ignoring order. In 1918 Hardy and Ramanujan proved that
is given asymptotically by
.
This is a major plot point in the new Ramanujan movie, where Ramanujan conjectures this result and MacMahon challenges him by agreeing to compute and comparing it to what this approximation gives. In this post I’d like to describe how one might go about conjecturing this result up to a multiplicative constant; proving it is much harder.
Verification
MacMahon computed using a recursion for
implied by the pentagonal number theorem, which makes it feasible to compute
by hand. Instead of doing it by hand I asked WolframAlpha, which gives
whereas the asymptotic formula gives
.
Ramanujan is shown getting closer than this in the movie, presumably using a more precise asymptotic.
How might we conjecture such a result? In general, a very powerful method for figuring out the growth rate of a sequence is to associate to it the generating function
and relate the behavior of , often for complex values of
, to the behavior of
. The most comprehensive resource I know for descriptions both of how to write down generating functions and to analyze them for asymptotic behavior is Flajolet and Sedgewick’s Analytic Combinatorics, and the rest of this post will follow that book’s lead closely.
The meromorphic case
The generating function strategy is easiest to carry out in the case that is meromorphic (for example, if it’s rational); in that case the asymptotic growth of
is controlled by the behavior of
near the pole (or poles) closest to the origin. For rational
this is particularly simple and just a matter of looking at the partial fraction decomposition.
Example.The generating function for the sequence of partitions into parts of size at most
is the rational function
whose most important pole is at and of order
, and whose other poles are at the
roots of unity, and of order at most
. We can factor
as
which gives, upon substituting , that the partial fraction decomposition begins
and hence, using the fact that
we conclude that is asymptotically
.
We ignored all of the other terms in the partial fraction decomposition to get this estimate, so there’s no reason to expect it to be particularly accurate unless is fairly large compared to
. Nonetheless, let’s see if we can learn anything from it about how big we should expect the partition function
itself to be. Taking logs and using the rough form
of Stirling’s approximation gives
and substituting for some
gives
.
If then this quantity is negative; at this point we’re clearly not in the regime where this approximation is accurate. If
then the first term dominates and we get something that grows like
. But if
then the first term vanishes and we get
.
This is at least qualitatively the correct behavior for , and the multiplicative constant isn’t so off either: the correct value is
.
Example. A weak order is like a total order, but with ties: for example, it describes a possible outcome of a horse race. Let denote the number of weak orders of
elements (the ordered Bell numbers, or Fubini numbers). General techniques described in Flajolet and Sedgewick can be used to show that
has exponential generating function
(which should be parsed as ; loosely speaking, this corresponds to a description of the combinatorial species of weak orders as the species of “lists of nonempty sets”). This is a meromorphic function with poles at
. The unique pole closest to the origin is at
, and we can compute using l’Hopital’s rule that
and hence the partial fraction decomposition of begins
which gives the asymptotic
Curiously, the error in the above approximation has some funny quasi-periodic behavior corresponding to the arguments of the next most relevant poles, at .
The saddle point bound
However, understanding meromorphic functions is not enough to handle the case of partitions, where the relevant generating function is
.
This function is holomorphic inside the unit disk but has essential singularities at every root of unity, and to handle it we will need a more powerful method known as the saddle point method, which is beautifully explained with pictures both in Flajolet and Sedgewick and in these slides, and concisely explained in these notes by Jacques Verstraete.
The starting point is that we can recover the coefficients of a generating function
using the Cauchy integral formula, which gives
where is a closed contour in
with winding number
around the origin and such that ;
is holomorphic in an open disk containing
. This integral can be straightforwardly bounded by the product of the length of
, denoted
, and the maximum value that
takes on it, which gives
.
From here, the name of the game is to attempt to pick such that this bound is as good as possible. For example, if we pick
to be the circle of radius
, then
. If
has nonnegative coefficients, which will always be the case in combinatorial applications, then
will take its maximum value when
, which gives the saddle point bound
as long as is holomorphic in an open disk of radius greater than
. Strictly speaking, this bound doesn’t require any complex analysis to prove: if
has nonnegative coefficients and
converges then for
we clearly have
.
But later we will actually use some complex analysis to improve the saddle point bound to an estimate.
The saddle point bound gets its name from what happens when we try to optimize this bound as a function of : we’re led to pick a value of
such that
is minimized (subject to the constraint that
is less than the radius of convergence
of
). This value will be a solution to the saddle point equation
and at such points the function , as a real-valued function of
, will have a saddle point. The saddle point equation can be rearranged into the more convenient form
and from here we can attempt to pick (which will generally depend on
) such that this equation is at least approximately satisfied, then see what kind of bound we get from doing so.
We’ll often be able to write for some nice
, in which case the saddle point equation simplifies further to
.
Example. Let ; we’ll use this generating function to get a lower bound on factorials. The saddle point bound gives
for any , since
has infinite radius of convergence. The saddle point equation gives
, which gives the upper bound
or equivalently the lower bound
.
We see that the saddle point bound already gets us within a factor of of the true answer.
This example has a probabilistic interpretation: the saddle point bound can be rearranged to read
which says that the probability that a Poisson random variable with rate takes the value
is at most
. When we take
we’re looking at the Poisson random variable with rate
, which for large
is concentrated around its mean
.
Example. Let denote the number of involutions (permutations squaring to the identity) on
elements. These are precisely the permutations consisting of cycles of length
or
, so the exponential formula gives an exponential generating function
.
The saddle point bound gives
for any , since as above
has infinite radius of convergence. The saddle point equation is
with exact solution
and using for simplicity gives
This approximation turns out to also only be off by a factor of from the true answer.
Example. The Bell numbers count the number of partitions of a set of
elements into disjoint subsets. They have exponential generating function
(which also admits a combinatorial species description: this is the species of “sets of nonempty sets”), which as above has infinite radius of convergence. The saddle point equation is
which is approximately solved when (a bit more precisely, we want something more like
, and it’s possible to keep going from here but let’s not), giving the saddle point bound
.
Edit, 11/10/20: I don’t know how far off this is from the true asymptotics. According to Wikipedia it appears to be off by at least an exponential factor.
Example. Now let’s tackle the example of the partition function . Its generating function
has radius of convergence , unlike the previous examples, so our saddle points
will be confined the interval
(between the pole of
at
and the essential singularity at
). The saddle point equation involves understanding the logarithmic derivative of
, so let’s try to understand the logarithm. (
previously appeared on this blog here as the generating function of the number of subgroups of
of index
, although that won’t be directly relevant here.) The logarithm is
and it will turn out to be convenient to rearrange this a little: expanding this out gives
and exchanging the order of summation gives
.
The point of writing in this way is to make the behavior as
very clear: we see that as
,
approaches
.
It turns out that as , the saddle point gets closer and closer to the essential singularity at
. Near this singularity we may as well for the sake of convenience replace
with
, which gives the approximate saddle point equation
.
This saddle point equation reinforces the idea that is close to
: the only way to solve it in the interval
is to take something like
, so we can ignore the
factor, which gives the approximate saddle point
.
and saddle point bound
.
From here we need an upper bound on and a lower bound on
to get an upper bound on
. Edit, 12/12/16: As Akshaj explains in the comments, the argument that was previously here regarding the lower bound on
was incorrect. Akshaj’s argument involving the Taylor series of log gives
As for the upper bound on , if
then
for
, hence
from which we conclude that
and hence that
which is off from the true answer.
Of course, without knowing a better method that in fact gives the true answer, we have no way of independently verifying that the saddle point bounds are as close as we’ve claimed they are. We need a more powerful idea to turn these bounds into asymptotics and recover our factors of .
Hardy’s approach
In the eighth of Hardy’s twelve lectures on Ramanujan’s work, he describes a more down-to-earth way to guess that
starting from the approximation
.
as . He first observes that
must grow faster than a polynomial but slower than an exponential: if
grew like a polynomial then
would have a pole of finite order at
, whereas if
grew like an exponential then
would have a singularity closer to the origin. Hence, in Hardy’s words, it is “natural to conjecture” that
for some and some
. From here he more or less employs a saddle point bound in reverse, estimating
based on the size of its largest term. It’s convenient to write so that this sum can be rewritten
so that, differentiating in , we see that the maximum occurs when
. We want to turn this into an estimate for
involving only
, so we want to eliminate
and use the approximation
, valid as
. This gives
(keeping in mind that is positive), so that
and
which altogether gives (again, approximating by its largest term)
for . Matching this up with
gives
and
hence .
The saddle point method
The saddle point bound, although surprisingly informative, uses very little of the information provided by the Cauchy integral formula. We ought to be able to do a lot better by picking a contour to integrate over such that we can, by analyzing the contour integral more closely, bound the contour integral
more carefully than just by the “trivial” bound .
From here we’ll still be looking at saddle points, but more carefully, as follows. Ignoring the length factor in the trivial bound, if we try to minimize
we’ll end up at a saddle point
of
(so we get a point very slightly different from above, where we used a saddle point of
). Depending on the geometry of the locations of the zeroes, poles, and saddle points of
, we can hope to choose
to be a contour that passes through this saddle point
in such a way that
is in fact maximized at
. This means that
should enter and exit the “saddle” around the saddle point in the direction of steepest descent from the saddle point.
If we pick carefully, and
has certain nice properties, we can furthermore hope that
- the contour integral over a small arc (in terms of the circle method, the “major arc”) is easy to approximate (usually by a Gaussian integral), and
- the contour integral over everything else (in terms of the circle method, the “minor arc”) is small enough that it’s easy to bound.
The Gaussian integrals that often appear when integrating over the major arc are responsible for the factors of we lost above.
Let’s see how this works in the case of the factorials, where . The function
has a unique saddle point at
, but to simplify the computation we’ll take
as before. We’ll take
to be the circle of radius
, which gives a contour integral which can be rewritten in polar coordinates as
.
This integral can also be thought of as coming from computing the Fourier coefficients of a suitable Fourier series. Write the integrand as , so that
.
only controls the phase of the integrand, and since it doesn’t vary much (it grows like
for small
) we’ll be able to ignore it.
controls the absolute value of the integrand and so is much more important. For small values of
we have
so from here we can try to break up the integral into a “major arc” where for some small (where the meaning of “small” depends on
)
and a “minor arc” consisting of the other values of
, and try to show both the integral over the major arc is well approximated by the Gaussian integral
and that the integral over the minor arc is negligible compared to this. This can be done, and the details are in Flajolet and Sedgewick (who take ); ignoring all the details, the conclusion is that
and hence that
which is exactly Stirling’s approximation. This computation also has a probabilistic interpretation: it says that the probability that a Poisson random variable with rate takes its mean value
is asymptotically
, which can be viewed as a corollary of the central limit theorem, since such a Poisson random variable is a sum of
independent Poisson random variables with rate
.
In general we’ll again find that, under suitable hypotheses, we can approximate the major arc integral by a Gaussian integral (using the same strategy as above) and bound the minor arc integral to show that it’s negligible. This gives the following:
Theorem (saddle point approximation): Under suitable hypotheses, if and
, let
be a saddle point of
, so that
. Then, as
, we have
.
Directly applying this theorem to the partition function is difficult because of the difficulty of bounding what happens on the minor arc. has essential singularities on a dense subset of the unit circle, and delicate analysis has to be done to describe the contributions of these singularities (or more precisely, of saddle points near these singularities); the circle method used by Hardy and Ramanujan to prove the asymptotic formula accomplishes this by choosing the contour
very carefully and then using modularity properties of
(which is closely related to the eta function).
We will completely ignore these difficulties and pretend that only the contribution from the (saddle point near the) essential singularity at matters to the leading term. Even ignoring the minor arc, to make use of the saddle point approximation requires that we know the asymptotics of
as
in more detail than we do right now.
Unfortunately there does not seem to be a really easy way to do this; Hardy’s approach uses the modular properties of the eta function, while Flajolet and Sedgewick use Mellin transforms. So at this point we’ll just quote without proof the asymptotic we need from Flajolet and Sedgewick, up to the accuracy we need, namely
.
Although this changes the location of the saddle point slightly, for ease of computation (and because it will lose us at worst multiplicative factors in the end) we’ll continue to work with the same approximate saddle point
as before. The saddle point approximation differs from the saddle point bound we established earlier in two ways: first, the introduction of the
term contributes a factor of
and second, the introduction of the denominator contributes another factor, which we approximate as follows. We have
and hence
so that
which gives (we actually know the multiplicative constant here, but it doesn’t matter because we already lost multiplicative constants when estimating
) and hence
.
Altogether the saddle point approximation, up to a multiplicative constant, is
.
There are some formulas that does not displayed. I think you might want to check the code again.
Thanks, I don’t know what happened but it’s fixed. At some point recently WordPress replaced a bunch of spaces in the text with “& nbsp ;” (no spaces) and it messed some stuff up.
In the section “The saddle point bound”, when lower bounding the terms of (with regards to the partition function), you seemed to have messed up an inequality (apologies if I am mistaken). I believe that for
(with regards to the partition function), you seemed to have messed up an inequality (apologies if I am mistaken). I believe that for  in the range
in the range  and not the other way around as you claim. This can be seen via the Taylor expansion of
and not the other way around as you claim. This can be seen via the Taylor expansion of 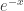 . Thus your lower bound is actually an upper bound. It is simple to rectify your error, however, as follows:
. Thus your lower bound is actually an upper bound. It is simple to rectify your error, however, as follows:
We shall upper bound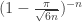 :
:
Then, Taylor expand the logarithm, and asymptotically only the first two terms contribute. If you do this out, you should get the bound .
.
This weakens the resulting bound by a constant factor of , but the exponential term will turn out to be the same. This is of course assuming I didn't make any stupid mistakes (I really hope!). Overall a great article though–fantastic exposition and blog post. I really learned a lot, thanks!
, but the exponential term will turn out to be the same. This is of course assuming I didn't make any stupid mistakes (I really hope!). Overall a great article though–fantastic exposition and blog post. I really learned a lot, thanks!
Yep, you’re right. Thanks for the correction! When you drop the rest of the Taylor series you don’t get an actual upper bound (you get an asymptotic for an upper bound) but this is straightforward to deal with.
[…] The man who knew elliptic integrals, prime number theorems, and black holes The man who knew partition asymptotics […]
[…] « The man who knew partition asymptotics […]