The p-group fixed point theorem

« Cantor’s theorem, the prisoner’s dilemma, and the halting problem

The p-group fixed point theorem

July 9, 2013 by Qiaochu Yuan

The goal of this post is to collect a list of applications of the following theorem, which is perhaps the simplest example of a fixed point theorem.

Theorem: Let $G$ be a finite $p$ -group acting on a finite set $X$ . Let $X^G$ denote the subset of $X$ consisting of those elements fixed by $G$ . Then $|X^G| \equiv |X| \bmod p$ ; in particular, if $p \nmid |X|$ then $G$ has a fixed point.

Although this theorem is an elementary exercise, it has a surprising number of fundamental corollaries.

Proof

$X$ is a disjoint union of orbits for the action of $G$ , all of which have the form $G/H$ and hence all of which have cardinality divisible by $p$ except for the trivial orbits corresponding to fixed points.

Some group-theoretic applications

Theorem: Let $G$ be a finite $p$ -group. Then its center $Z(G)$ is nontrivial.

Corollary: Every finite $p$ -group is nilpotent.

Proof. $G$ acts by conjugation on $G \setminus \{ 1 \}$ . If $|G| = p^n$ , this set has cardinality $p^n - 1$ , which is not divisible by $p$ . Hence $G$ has a fixed point, which is precisely a nontrivial central element. $\Box$

Cauchy’s theorem: Let $G$ be a finite group. Suppose $p$ is a prime dividing $|G|$ . Then $G$ has an element of order $p$ .

Proof. $\mathbb{Z}/p\mathbb{Z}$ acts by cyclic shifts on the set

$\{ (g_1, g_2, ... g_p) \in G^p : g_1 g_2 ... g_p = 1 \} \setminus \{ (1, 1, ... 1) \in G^p \}$

since if $g_1 g_2 ... g_p = 1$ then $g_p (g_1 g_2 ... g_p) g_p^{-1} = 1$ . This set has cardinality $|G|^{p-1} - 1$ , which is not divisible by $p$ , hence $\mathbb{Z}/p\mathbb{Z}$ has a fixed point, which is precisely a nontrivial element $g \in G$ such that $g^p = 1$ . $\Box$

Some number-theoretic applications

Fermat’s little theorem: Let $a$ be a non-negative integer and $p$ be a prime. Then $a^p \equiv a \bmod p$ .

Proof. $\mathbb{Z}/p\mathbb{Z}$ acts by cyclic shifts on the set $[a]^p$ , where $[a] = \{ 1, 2, ... a \}$ ; equivalently, on the set of strings of length $p$ on $a$ letters. (Orbits of this group action are sometimes called necklaces; see, for example, this previous blog post.) This set has cardinality $a^p$ and its fixed point set has cardinality $a$ , since a function is fixed if and only if it is constant. $\Box$

Fermat’s little theorem for matrices: Let $A$ be a square matrix of non-negative integers and let $p$ be a prime. Then $\text{tr}(A^p) \equiv \text{tr}(A) \bmod p$ .

This result also appeared in this previous blog post.

Proof. Interpret $A$ as the adjacency matrix of a graph. $\mathbb{Z}/p\mathbb{Z}$ acts by cyclic shifts on the set of closed walks of length $p$ on this graph. This set has cardinality $\text{tr}(A^p)$ and its fixed point set has cardinality $\text{tr}(A)$ , since a closed walk is fixed if and only if it consists of $p$ repetitions of the same loop at a vertex. $\Box$

In the same way that Fermat’s little theorem can be used to construct a primality test, the Fermat primality test, Fermat’s little theorem for matrices can also be used to construct a primality test, which doesn’t seem to have a name. For example, the Perrin pseudoprimes are the numbers that pass this test when

$\displaystyle A = \left[ \begin{array}{ccc} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 1 & 0 \end{array} \right]$ .

More generally, a stronger version of this test gives rise to the notion of Frobenius pseudoprime.

Wilson’s theorem: Let $p$ be a prime. Then $(p-1)! \equiv -1 \bmod p$ .

Proof. Consider the set of total orderings of the numbers $\{ 0, 1, 2, ... p-1 \}$ modulo addition $\bmod p$ ; that is, we identify the total ordering

$\displaystyle a_0 < a_1 < ... < a_{p-1}$

with the total ordering

$\displaystyle a_0 + k < a_1 + k < ... < a_{p-1} + k$

where the addition occurs $\bmod p$ .

$\mathbb{Z}/p\mathbb{Z}$ acts by cyclic shifts on this set. It has cardinality $(p-1)!$ and its fixed point set has cardinality $p-1$ , since the fixed orderings are precisely the ones such that $a_{i+1} \equiv a_i + k \bmod p$ for some $k \in \{ 1, 2, ... p-1 \}$ . $\Box$

Lucas’ theorem: Let $m, n$ be non-negative integers and $p$ be a prime. Suppose the base- $p$ expansions of $m, n$ are

$\displaystyle m = \sum_i m_i p^i, n = \sum n_i p^i$

respectively. Then

$\displaystyle {m \choose n} \equiv \prod_i {m_i \choose n_i} \bmod p$ .

Proof. It suffices to show that

$\displaystyle {m_0 + p m_1 \choose n_0 + p n_1} \equiv {m_0 \choose n_0} {m_1 \choose n_1} \bmod p$

where $0 \le m_0, n_0 < p$ , and then the desired result follows by induction. To see this, consider a set $S$ of size $m_0 + p m_1$ , and partition it into a block of size $m_0$ together with $p$ blocks of size $m_1$ . Identify all of the $p$ blocks of size $m_1$ with each other in some way. Then $\mathbb{Z}/p\mathbb{Z}$ acts by cyclic shift on these blocks. This action extends to an action on the set of subsets of $S$ of size $n_0 + p n_1$ . A fixed point of this action consists of a subset of the block of size $m_0$ together with $p$ copies of a subset of any block of size $m_1$ . Since the union of the $p$ copies has size divisible by $p$ , and since $m_0 < p$ , it follows that there must be $n_0$ elements in the block of size $m_0$ and $n_1$ elements in each of the $p$ blocks. Thus the set of subsets has cardinality ${m_0 + p m_1 \choose n_0 + p n_1}$ , and its fixed point set has cardinality ${m_0 \choose n_0} {m_1 \choose n_1}$ . $\Box$

(It is also possible to prove this result directly by considering a more complicated $p$ -group action. The relevant $p$ -group is the Sylow $p$ -subgroup of the symmetric group of $S$ . It is an iterated wreath product of the cyclic groups $\mathbb{Z}/p\mathbb{Z}$ , and describing how it acts on $S$ requires recursively partitioning blocks in a way that is somewhat tedious to describe.)

The following proof is due to Don Zagier.

Fermat’s two-square theorem: Every prime $p \equiv 1 \bmod 4$ is the sum of two squares.

Proof. Let $S$ be the set of all solutions $(x, y, z)$ in the positive integers of the equation $x^2 + 4yz = p$ . The involution $(x, y, z) \mapsto (x, z, y)$ has the property that its fixed points correspond to solutions to the equation $x^2 + 4y^2 = p$ . We will show that such fixed points exist by showing that there are an odd number of them; to do so, it suffices to show that $|S|$ is odd, and to show that $|S|$ is odd it suffices to exhibit any other involution on $S$ which has an odd number of fixed points. (Notice that this is two applications of the $2$ -group fixed point theorem.) We claim that

$\displaystyle (x, y, z) \mapsto \begin{cases} (x + 2z, z, y - z - x) & \text{ if } x < y - z \\ (2y - x, y, x - y + z) & \text{ if } y - z < x < 2y \\ (x - 2y, x - y + z, y) & \text{ if } x > 2y \end{cases}$

is an involution on $S$ with exactly one fixed point, which suffices to prove the desired claim. Verifying that it sends $S$ to $S$ is straightforward. If $(x', y', z')$ is a fixed point, then since $x', y', z'$ are all assumed to be positive integers we cannot have $x' = x' + 2z'$ , so we are not in the first case. If we are in the second case, we conclude that $x' = y'$ , but then $x' | p$ , and since $x' \le \sqrt{p}$ we conclude that $x' = y' = 1$ , which gives $z' = \frac{p-1}{4}$ . If we are in the third case, we conclude that $y' = z'$ , then that $x' = y'$ , but this contradicts $x' > 2y'$ . Hence $(1, 1, \frac{p-1}{4})$ is the unique fixed point as desired. $\Box$

The following proof is due to V. Lebesgue.

Quadratic reciprocity: Let $p, q$ be odd primes. Let $\left( \frac{p}{q} \right)$ denote the Legendre symbol. Then

$\displaystyle \left( \frac{p}{q} \right) = \left( \frac{q}{p} \right) (-1)^{ \frac{(p-1)(q-1)}{4} }$ .

Proof. Let $p$ be an odd prime and consider the set

$\displaystyle S_n(p, a) = \{ (x_1, ... x_n) \in \mathbb{F}_p^n : x_1^2 + ... + x_n^2 = a \}$ .

For $q$ an odd prime, we will compute $|S_q(p, 1)| \bmod q$ in two different ways. The first way is to observe that $\mathbb{Z}/q\mathbb{Z}$ acts by cyclic shifts on $S_q(p, 1)$ . The number of fixed points is the number of $x \in \mathbb{F}_p$ such that $qx^2 = 1$ , hence

$\displaystyle |S_q(p, 1)| \equiv 1 + \left( \frac{q}{p} \right) \bmod q$ .

The second way is to find a recursive formula for $|S_n(p, 1)|$ which will end up being expressed in terms of $\left( \frac{p}{q} \right)$ . The details are as follows.

First, it is clear that $|S_1(p, a)| = 1 + \left( \frac{a}{p} \right)$ . For $a$ nonzero, we claim that $|S_2(p, a)|$ is independent of $a$ . First, observe that by the pigeonhole principle (there are $\frac{p+1}{2}$ possible values of $x_1^2$ and $\frac{p+1}{2}$ possible values of $a - x_2^2$ , hence at least one common value) we always have $|S_2(p, a)| > 0$ . Second, observe that the map $(x_1, x_2) \mapsto x_1^2 + x_2^2$ is the norm map from $\mathbb{F}_p[i]/(i^2 + 1)$ to $\mathbb{F}_p$ ; in particular, it restricts to a homomorphism from the unit group of the former ring to the unit group of the latter ring, and we know that this homomorphism is surjective, so each fiber has the same size. The unit group of $\mathbb{F}_p[i]/(i^2 + 1)$ has size $p^2 - 1$ if $p \equiv 3 \bmod 4$ (since then we are looking at $\mathbb{F}_{p^2}$ ) and size $(p - 1)^2$ if $p \equiv 1 \bmod 4$ (since then we are looking at $\mathbb{F}_p \times \mathbb{F}_p$ ). Hence

$\displaystyle |S_2(p, a)| = p - (-1)^{\frac{p-1}{2}}$

for any nonzero $a$ . When $a = 0$ , the equation $x_1^2 + x_2^2 = 0$ always has the solution $(0, 0)$ . There are no nonzero solutions if $p \equiv 3 \bmod 4$ (since $-1$ does not have a square root) and $2p - 2$ nonzero solutions if $p \equiv 1 \bmod 4$ (since for each of the $p-1$ possible values of $x_1$ there are $2$ possible values of $x_2$ ). Hence

$\displaystyle |S_2(p, 0)| = p + (p-1)(-1)^{ \frac{p-1}{2} }$ .

We will now compute $|S_n(p, a)|$ inductively by rewriting $x_1^2 + ... + x_n^2 = a$ as

$\displaystyle x_1^2 + ... + x_{n-2}^2 = a - x_{n-1}^2 - x_n^2$ .

From this it follows that

$\displaystyle |S_n(p, a)| = \sum_{x_{n-1}, x_n = 0}^{p-1} |S_{n-2}(p, a - x_{n-1}^2 - x_n^2)|$ .

We know that $a - x_{n-1}^2 - x_n^2$ takes the value $a$ for $p + (p-1)(-1)^{ \frac{p-1}{2} }$ possible values of $(x_{n-1}, x_n)$ and takes any particular other value for $p - (-1)^{ \frac{p-1}{2} }$ possible values of $(x_{n-1}, x_n)$ . Hence we can write

$\displaystyle |S_n(p, a)| = \left( p - (-1)^{ \frac{p-1}{2} } \right) \sum_{b=0}^{p-1} |S_{n-2}(p, b)| + p (-1)^{ \frac{p-1}{2} } |S_{n-2}(p, a)|.$

But it’s clear that

$\displaystyle \sum_{b=0}^{p-1} |S_{n-2}(p, b)| = p^{n-2}$

since this is just the number of possible tuples $(x_1, ... x_{n-2})$ . Hence

$\displaystyle |S_n(p, a)| = p^{n-1} - p^{n-2} (-1)^{ \frac{p-1}{2} } + p (-1)^{ \frac{p-1}{2} } |S_{n-2}(p, a)|$ .

This gives a recursion which we can unwind into an explicit formula for $|S_n(p, a)|$ as follows. Substituting the recursion into itself and canceling terms gives

$\displaystyle |S_n(p, a)| = p^{n-1} - p^{n-3} (-1)^{ 2 \frac{p-1}{2} } + p^2 (-1)^{ 2 \frac{p-1}{2} } |S_{n-4}(p, a)|$ .

This pattern continues, and by induction we can show that

$\displaystyle |S_n(p, a)| = p^{n-1} - p^{n-1-k} (-1)^{ k \frac{p-1}{2} } + p^k (-1)^{ k \frac{p-1}{2} } |S_{n-2k}(p, a)|$ .

Hence if $n = 2k+1$ is odd, we conclude that

$\displaystyle |S_{2k+1}(p, 1)| = p^{2k} + p^k (-1)^{ k \frac{p-1}{2} }$ .

Now let $2k+1 = q$ be an odd prime. Then $p^{2k} = p^{q-1} \equiv 1 \bmod q$ by Fermat’s little theorem and $p^k = p^{\frac{q-1}{2}} \equiv \left( \frac{p}{q} \right) \bmod q$ by Euler’s criterion, so we we find that

$\displaystyle |S_q(p, 1)| \equiv 1 + \left( \frac{p}{q} \right) (-1)^{ \frac{(p-1)(q-1)}{4} } \bmod q$ .

On the other hand, we know that $|S_q(p, 1)| \equiv 1 + \left( \frac{q}{p} \right) \bmod q$ . We conclude that

$\displaystyle \left( \frac{q}{p} \right) \equiv \left( \frac{p}{q} \right) (-1)^{ \frac{(p-1)(q-1)}{4} } \bmod q$

and since the LHS and RHS are both equal to $\pm 1$ this equality holds on the nose. $\Box$

This proof is in some sense a proof via Gauss sums in disguise; the numbers $|S_n(p, a)|$ are closely related to Jacobi sums, which can be written in terms of Gauss sums. More generally, various kinds of exponential sums can be related to counting points on varieties over finite fields. The Weil conjectures give bounds on the latter which translate into bounds on the former, and this has various applications, for example the original proof of Zhang’s theorem on bounded gaps between primes (although my understanding is that this step is unnecessary just to establish the theorem).

Similar methods can be used to prove the second supplementary law, although strictly speaking we will use more than the $p$ -group fixed point theorem.

Quadratic reciprocity, second supplement: $\displaystyle \left( \frac{2}{p} \right) = (-1)^{ \frac{p^2-1}{8} }$ . Equivalently, $\displaystyle \left( \frac{2}{p} \right) = 1$ iff $p \equiv \pm 1 \bmod 8$ .

Proof. We will compute $|S_2(p, 1)| \bmod 8$ in two different ways. The first is using the formula $|S_2(p, 1)| = p - (-1)^{ \frac{p-1}{2} }$ we found earlier, which gives

$\displaystyle |S_2(p, 1)| \equiv \begin{cases} 0 \bmod 8 \text{ if } p \equiv 1 \bmod 8 \\ 4 \bmod 8 \text{ if } p \equiv 3 \bmod 8 \\ 4 \bmod 8 \text{ if } p \equiv 5 \bmod 8 \\ 0 \bmod 8 \text{ if } p \equiv 7 \bmod 8 \\ \end{cases}$ .

The second is to observe that the dihedral group $D_4$ of order $8$ acts on $S_2(p, 1)$ by rotation and reflection (thinking of the points as being on the “circle” defined by $x_1^2 + x_2^2 = 1$ ). Most orbits of this action have size $8$ and hence are invisible $\bmod 8$ . The ones that are not invisible $\bmod 8$ correspond to points with some nontrivial stabilizer. Any stabilizer contains an element of order $2$ , and there are five such elements in $D_4$ , so the remaining possible orbits are as follows:

Points stable under $(x, y) \mapsto (y, x)$ . These are precisely the points $(x, x)$ such that $2x^2 = 1$ , hence there are $1 + \left( \frac{2}{p} \right)$ of them.
Points stable under $(x, y) \mapsto (x, -y)$ . These are precisely the points $(x, 0)$ such that $x^2 = 1$ , hence there are $2$ of them.
Points stable under $(x, y) \mapsto (-x, y)$ . These are precisely the points $(y, 0)$ such that $y^2 = 1$ , hence there are $2$ of them.
Points stable under $(x, y) \mapsto (-x, -y)$ . There are no such points.
Points stable under $(x, y) \mapsto (-y, -x)$ . These are precisely the points $(x, -x)$ such that $2x^2 = 1$ , hence there are $1 + \left( \frac{2}{p} \right)$ of them.

In total, we conclude that

$\displaystyle 6 + 2 \left( \frac{2}{p} \right) \equiv \begin{cases} 0 \bmod 8 \text{ if } p \equiv 1 \bmod 8 \\ 4 \bmod 8 \text{ if } p \equiv 3 \bmod 8 \\ 4 \bmod 8 \text{ if } p \equiv 5 \bmod 8 \\ 0 \bmod 8 \text{ if } p \equiv 7 \bmod 8 \\ \end{cases}$

and the conclusion follows. $\Box$

A general lesson of the above proofs is that it is a good idea to replace integers with sets because sets can be equipped with more structure, such as group actions, than integers. This is a simple form of categorification.

Posted in math.CO, math.GR, math.NT | Tagged finite fields, fixed point theorems, group actions, walks on graphs | 13 Comments

13 Responses

on November 1, 2020 at 3:44 pm | Reply Meditation on the Sylow theorems I | Annoying Precision

[…] -group fixed point theorem (PGFPT): If is a finite -group and is a finite set on which acts, then the subset of fixed […]
on October 4, 2013 at 5:22 pm | Reply Benjamin Steinberg

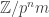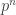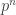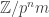Here is one I like to use when I prove the Sylow theorems via Wielandt’s proof. If $p$ , then $\binom{p^nm}{p^n}\cong m\mod p$ . The proof is let $H$ be the subgroup of $\mathbb Z/p^nm$ of order $p^n$ and have it act on the subsets of size $p^n$ of $\mathbb Z/p^nm$ by translations. Then clearly the fixed points are the $m$ cosets of $H$ . The fixed point theorem gives the desired conclusion.

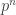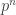Now to get the Sylow theorems let $G$ be a group of order $p^nm$ with $(p,m)=1$ . Then $G$ acts on the set $X$ of its subsets of order $p^n$ by translation. By the above paragraph, $p$ does not divide the size of $X$ and so not all stabilizers have index divisible by $p$ . Let $Y$ be a subset of size $p^n$ whose stabilizer $H$ has index prime to $p$ . Since $H$ acts freely on $Y$ it follows the order of $H$ is a $p$ -power so we conclude $H$ is a $p$ -Sylow subgroup.
on July 30, 2013 at 2:46 pm | Reply xinkeguoxue

Can you explain why the last sentence implies the claim?
- on July 30, 2013 at 3:26 pm | Reply Qiaochu Yuan
  
  The last sentence of the proof of Wilson’s theorem? Apply the fixed point theorem.
on July 30, 2013 at 12:51 pm | Reply xinkeguoxue

for wilson theorem proof, why does cardinality of fixed point set equal cardinality of set itself?
- on July 30, 2013 at 12:53 pm | Reply Qiaochu Yuan
  
  It doesn’t. The claim is just that they’re equivalent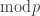 $\bmod p$ .
on July 22, 2013 at 1:54 am | Reply Robin Whitty

Perhaps the following deserves a mention? P.G. Anderson, A.T. Benjamin and J.A. Rouse “, ‘Combinatorial Proofs of Fermat’s, Lucas’s, and Wilson’s Theorems”, American Mathematical Monthly, 115, 2005, 266–268.
- on July 22, 2013 at 2:33 pm | Reply Qiaochu Yuan
  
  Thanks for the reference! I wasn’t aware of it. My understanding is that the Lucas proof is well-known (at least, it’s on the Wikipedia article) but I didn’t know a reference for the Fermat or Wilson proofs.
on July 9, 2013 at 4:07 pm | Reply KCd

Since the application to the main law of quadratic reciprocity only requires the case of $S_n(a,p)$ for odd $n$, I think you should work out that case first and separately from the case of even $n$. After proving the main law of QR, come back and work out the formula for even $n$.
- on July 9, 2013 at 4:19 pm | Reply Qiaochu Yuan
  
  But don’t I need $S_2$ to get the induction to work?
  - on July 10, 2013 at 6:10 am | Reply KCd
    
    Yes, just $S_2$ among even-indexed cases is needed. You don’t need $S_n$ for even $n > 2$. I meant to suggest delaying the even case for $n > 2$.
on July 9, 2013 at 1:52 pm | Reply cc

also: mod p irreps of p-groups can only be trivial
- on July 9, 2013 at 3:16 pm | Reply Qiaochu Yuan
  
  Yes, this is a nice application too (the set of nonzero vectors in a finite-dimensional vector space over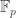 $\mathbb{F}_p$ has cardinality not divisible by $p$ so any $p$ -group representation on such a vector space has a fixed point, hence an eigenvector), and draws attention to an interesting analogy between finite $p$ -groups and solvable linear algebraic groups in light of the Lie-Kolchin theorem.

Comments RSS

	ZW on The double commutant theo…
	auto on More about the Schrödinger equ…
	Jaromir Kuben on Meditation on the Sylow theore…
	Qiaochu Yuan on Meditation on the Sylow theore…
	Qiaochu Yuan on Some remarks on the infinitude…

Annoying Precision

"A good stock of examples, as large as possible, is indispensable for a thorough understanding of any concept, and when I want to learn something new, I make it my first job to build one." – Paul Halmos

Recent Comments

Blogroll

Categories

Archives

Tag Cloud

Annoying Precision

"A good stock of examples, as large as possible, is indispensable for a thorough understanding of any concept, and when I want to learn something new, I make it my first job to build one." – Paul Halmos