As an undergraduate the proofs I saw of the Sylow theorems seemed very complicated and I was totally unable to remember them. The goal of this post is to explain proofs of the Sylow theorems which I am actually able to remember, several of which use our old friend
The -group fixed point theorem (PGFPT): If
is a finite
-group and
is a finite set on which
acts, then the subset
of fixed points satisfies
. In particular, if
then this action has at least one fixed point.
There will be some occasional historical notes taken from Waterhouse’s The Early Proofs of Sylow’s Theorem.
A quick note on the definition of a Sylow subgroup
A Sylow -subgroup of a finite group
can be equivalently defined as either a
-subgroup of index coprime to
(that is, if
where
, then
) or a
-subgroup which is maximal with respect to inclusion. The equivalence of these two definitions requires the Sylow theorems, but we’ll want to discuss such subgroups before proving them, and for the purposes of this post it will be most convenient to adopt the first definition.
So for the rest of this post, a Sylow -subgroup is a
-subgroup of index coprime to
, and we’ll refer to
-subgroups maximal with respect to inclusion as maximal
-subgroups before we prove that the two are equivalent.
Warmup: Cauchy’s theorem
We’ll start off by giving some proofs of Cauchy’s theorem. One of the proofs of Sylow I later needs it as a lemma, and some of the proofs we give here will generalize to proofs of Sylow I. First we quote the proof using the PGFPT in full from the above blog post, as Proof 1.
Cauchy’s theorem: Let be a finite group. Suppose
is a prime dividing
. Then
has an element of order
.
Proof 1 (PGFPT). acts by cyclic shifts on the set
since if then
. This set has cardinality
, which is not divisible by
, hence
has a fixed point, which is precisely a nontrivial element
such that
.
This proof is almost disgustingly short. By contrast, according to Waterhouse, Cauchy’s original proof runs nine pages (!) and works as follows.
First Cauchy explicitly constructs Sylow -subgroups of the symmetric group
. This can be done by recursively partitioning
into
blocks of size
, considering the subgroup generated by
-cycles cyclically permuting each block, then partitioning the set of blocks itself into
blocks-of-blocks of size
, cyclically permuting these, and so forth. This subgroup has size
and the exponent is Legendre’s formula for the largest power of
dividing
. It follows that this is a Sylow
-subgroup.
Second, Cauchy proves a special case of the following lemma, namely the special case that . This lemma doesn’t appear to have a standard name, so we’ll name it
Cauchy’s -group lemma: Let
be a subgroup of a finite group
such that
has a Sylow
-subgroup
. If
, then
has an element of order
.
Proof. We’ll prove the contrapositive: if doesn’t contain an element of order
, then
does not divide
.
Consider the left action of on the set of cosets
. By grouping the cosets into
-orbits and using the orbit-stabilizer theorem we have
where is the collection of double cosets and the stabilizer of a coset is
and in particular it has order dividing , hence a power of
.
If has no element of order
, then since any nontrivial subgroup of
contains an element of order
, these stabilizers are all trivial, so we get that
and in particular that divides
. Since
is a Sylow
-subgroup,
isn’t divisible by
, and hence neither is
.
Call a collection of finite groups cofinal if every finite group embeds into at least one of them.
Corollary: To prove Cauchy’s theorem for all finite groups, it suffices to find a cofinal collection of finite groups which have Sylow -subgroups.
We can now complete Cauchy’s proof of Cauchy’s theorem.
Proof 2 (symmetric groups). The symmetric groups are cofinal (this is exactly Cayley’s theorem) and have Sylow
-subgroups.
But we don’t have to use the symmetric groups!
Proof 3 (general linear groups). Since the symmetric groups embed into the general linear groups
, the latter are also cofinal, and we can also exhibit Sylow
-subgroups for them: the unipotent subgroup
of upper triangular matrices with
s on the diagonal is Sylow. This follows from the standard calculation of the order
where is the
-factorial.
Here’s a fourth proof that doesn’t use Cauchy’s lemma and doesn’t require the clever construction of the first proof; Waterhouse says it’s used by Rotman.
Proof 4 (class equation). We induct on the order of . First we observe that Cauchy’s theorem is straightforwardly true for finite abelian groups by using the Chinese remainder theorem to write a finite abelian group as a direct sum of finite abelian
-groups. (And then, to spell it out very explicitly, Lagrange’s theorem implies that any nontrivial element of a finite
-group has
-power order, so some power of that element has order
.)
Next, given a finite group such that
we consider the class equation
where the sum runs over non-central conjugacy classes. If then we’re done by reduction to the abelian case. Otherwise,
doesn’t divide
but does divide
, so by taking both sides
we conclude that there is some
such that the centralizer
has index in
coprime to
, and hence
. Since
is a non-central conjugacy class
has order strictly less than
so has an element of order
by the inductive hypothesis.
Sylow I
With very little additional effort the above proof of Cauchy’s -group lemma actually proves the following stronger result; Waterhouse attributes this argument, again in the special case that
, to Frobenius. It also doesn’t appear to have a standard name, so we’ll call it
Frobenius’ -group lemma: Let
be a subgroup of a finite group
such that
has a Sylow
-subgroup
. Then
also has a Sylow
-subgroup, given by its intersection with some conjugate of
.
Proof. Consider as before the sum
obtained by considering the orbits of the action of on
. Since
doesn’t divide
, at least one term on the RHS is also not divisible by
, so there exists some
such that
has index coprime to
and hence is a Sylow
-subgroup of
; conjugating, we get that the intersection of
with
is a Sylow
-subgroup of
as desired.
Corollary: To prove that Sylow subgroups exist for all finite groups, it suffices to prove that they exist for a cofinal collection of finite groups.
Now we can give two different proofs of Sylow I, as follows.
Sylow I: Every finite group has a Sylow
-subgroup.
(Note that with our definitions if then this subgroup is just the trivial group.)
Proof 1 (symmetric groups). It suffices to prove the existence of Sylow subgroups for the symmetric groups , which was done above.
Proof 2 (general linear groups). It suffices to prove the existence of Sylow -subgroups for
, which was done above. Running the argument gives that every finite
-group is a subgroup of
for some
, which gives an independent proof that finite
-groups are nilpotent.
Proof 2 is the first proof of Sylow I given by Serre in his Finite Groups: An Introduction.
I heard a rumor years ago that these proofs existed but didn’t see them; glad that’s finally settled.
The next proof of Sylow I we’ll present is the one that I saw as an undergraduate, in Artin’s Algebra if memory serves. According to Wikipedia it’s due to Wielandt. Serre attributes it to “Miller-Wielandt” and it’s the second proof he gives.
Proof 3 (action on subsets). Write where
and consider the action of
by left multiplication on the set
of
-element subsets of
. We’ll show that there exists a stabilizer subgroup of size
.
(I found this construction very bizarre and unmotivated as an undergraduate. I like it better now, I guess, but I’m still a little mystified.)
Key observation: An element stabilizes a subset
iff
consists of cosets of the cyclic subgroup
generated by
; in particular a necessary condition is that its order must divide the size of
.
This means that the action of on
has the property that all stabilizers must be
-groups (just like the action of
on
we used above). As before, decomposing this action into orbits gives
where the sum runs over a set of orbit representatives.
Lemma: .
Proof. This is a special case of Lucas’ theorem, which we proved using the PGFPT previously.
It follows that is not divisible by
, so there exists some subset
such that
is also not divisible by
. But since
is a power of
this is only possible if
. This stabilizer is a Sylow
-subgroup as desired.
This proof is tantalizingly similar to the proof of Frobenius’ lemma above; in both cases the key is to write down an action of on a set of size relatively prime to
but such that all stabilizers must be
-groups. But I’m not yet sure how to relate them.
We’re not done with proofs of Sylow I! The next proof is due to Frobenius; Waterhouse stresses that its early use of quotients crucially highlighted the importance of working with abstract groups rather than just groups of substitutions as was standard in early group theory. It generalizes the class equation proof of Cauchy’s theorem above.
Proof 4 (class equation). We again induct on the order of and start by observing that Sylow subgroups clearly exist for finite abelian groups, for example by the structure theorem. We can also use the Chinese remainder theorem.
Now, suppose that . If
also divides the order
of the center, then
contains a (central, abelian, nontrivial) Sylow
-subgroup
, which we can quotient by. Then
, by the inductive hypothesis, also contains a Sylow
-subgroup, and the preimage of this subgroup is a Sylow
-subgroup of
.
If , then again we inspect the class equation
where again the sum runs over non-central conjugacy classes. Since we conclude that there is some conjugacy class
such that
, hence such that
and
have the same
-adic valuation. By the inductive hypothesis,
contains a Sylow
-subgroup, which is then (by virtue of having the appropriate order) also a Sylow
-subgroup of
.
This proof is the first one we’ve seen that provides a halfway reasonable algorithm for finding Sylow subgroups, which is lovely (the first three are more or less just raw existence proofs): pass to the quotient by central -groups until you can’t anymore, then search for conjugacy classes whose centralizers have index relatively prime to
and pass to the centralizers until you can’t anymore, then repeat.
We give one final proof. According to Waterhouse, this one is essentially Sylow’s original proof, and it naturally proves an apparently-slightly-stronger result, interpolating between Cauchy’s theorem and Sylow I. It also provides a (different) algorithm for finding Sylow subgroups.
Sylow I+: Every finite group contains a subgroup of prime power order
whenever
. These subgroups can be constructed inductively by starting from an element of order
and then finding an element of
-power order normalizing the previous subgroup.
(Note that this result is equivalent to Sylow I as usually stated once we know that finite -groups admit composition series in which each quotient is
, which is not hard to prove by induction once we know that finite
-groups have nontrivial center, which in turn we proved previously using the PGFPT. The below proof actually gives an independent proof of the existence of such a composition series, and hence an independent proof that finite
-groups are nilpotent.)
Proof 5 (normalizers + PGFPT). We induct on . The base case
is Cauchy’s theorem, which we proved above (four times!).
Now suppose we’ve found a subgroup of order
, and we’d like to see if we can find a subgroup of order
. Consider the action of
by left multiplication on the cosets
. By the PGFPT the number of fixed points of this action satisfies
.
On the other hand, the fixed points of this action are precisely the cosets such that
, or equivalently such that
. So they are naturally in bijection with the quotient
of the normalizer
of . So the PGFPT tells us:
Lemma: If is a
-subgroup of a finite group
, then
.
If , or equivalently if
is not a Sylow
-subgroup, then
and hence
, so by Cauchy’s theorem it follows that
has an element
of order
. The preimage of the cyclic subgroup
in
is then a
-subgroup of order
as desired; more specifically it’s a subgroup
given by some extension
where generates the copy of
. So we’ve found our bigger
-subgroup.
This proof gives us an algorithm for finding Sylow subgroups by starting with elements of order and repeatedly finding elements of order
in the normalizer, and note that it also gives us a way to prove that a
-subgroup is Sylow without explicitly checking that its index is coprime to
:
Corollary (normalizer criterion): A -subgroup
of a finite group
is a Sylow
-subgroup iff the quotient
contains no elements of order
.
It has another corollary we haven’t quite gotten around to proving yet:
Corollary (Sylow = maximal): Sylow -subgroups are precisely the maximal
-subgroups.
(Before it could have been the case that there were -subgroups maximal with respect to inclusion but without index coprime to
.)
These are all the proofs of Sylow I that I know or could track down. After having gone through all of them I think I like proof 4 (class equation) and proof 5 (normalizers) the best. Proof 3 (action on subsets) is really too opaque and too specialized; you only learn from it that Sylow subgroups exist and practically nothing else, whereas proof 4 and proof 5 both teach you more about them, including how to find them. I’m sort of amazed it took me over 10 years after I first ran into the Sylow theorems to finally see a version of Sylow’s original proof, and that when I did, I liked it so much better than the first proof I had seen.
Sylow II and III
These will be short.
Sylow II: Let be a finite group and
be any Sylow
-subgroup. Every
-subgroup
of
is contained in a conjugate of
. In particular, taking
to be another Sylow
-subgroup, every pair of Sylow
-subgroups is conjugate.
Proof 1. Immediate corollary of Frobenius’ lemma.
Proof 2. Consider the action of on
. By hypothesis,
, so by the PGFPT,
.
A fixed point of the action of on
is precisely a coset
such that
, or equivalently such that
, so there must be at least one such
conjugating
into
as desired.
Corollary (Sylow = maximal, again): Sylow -subgroups are precisely the maximal
-subgroups.
(We’ve now proved this result in three different ways!)
Sylow III: Let be a finite group and
be any Sylow
-subgroup. The number
of Sylow
-subgroups of
satisfies
and
; in particular,
.
Proof. Since the Sylow -subgroups are conjugate, the set of Sylow
-subgroups is just the set of conjugates of
.
acts transitively on this set by conjugation with stabilizer
, so by orbit-stabilizer it has size
and in particular has size dividing
. We now give two proofs of the all-important congruence
.
Subproof 1 (action of on
). In Proof 5 (normalizers + PGFPT) of Sylow I above we showed that
and dividing both sides by gives the desired result.
Subproof 2 (action of on
). This proof has the benefit of explaining what this congruence “means.”
can’t be divisible by
, so the only elements of
-power order that normalize
are the elements of
, and the same must be true for any other Sylow. This implies that if we restrict the conjugation action of
on the Sylows to
, then
fixes only itself, so by the PGFPT
and the conclusion follows.
[…] « Meditation on the Sylow theorems I […]
That’s a nice exposition, just wanted to point out couple of things.
In the proof of Cauchy via the class equation you write “Cauchy’s theorem is straightforwardly true for finite abelian groups by using the Chinese remainder theorem to write a finite abelian group as a direct sum of finite abelian -groups. (And then, to spell it out very explicitly, Lagrange’s theorem implies that any nontrivial element of a finite
-groups. (And then, to spell it out very explicitly, Lagrange’s theorem implies that any nontrivial element of a finite  -group has
-group has  -power order, so some power of that element has order
-power order, so some power of that element has order  .).” If I read this correctly (correct me if I don’t) then this assumes that you already know that finite abelian groups are product of finite cyclic groups. However that not necessary since we can prove it directly by induction on the group order. Indeed, let
.).” If I read this correctly (correct me if I don’t) then this assumes that you already know that finite abelian groups are product of finite cyclic groups. However that not necessary since we can prove it directly by induction on the group order. Indeed, let  be a finite abelian group with
be a finite abelian group with  and pick random
and pick random 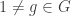 . If
. If 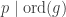 then we’re done, otherwise we pass to
then we’re done, otherwise we pass to  which contains an element of order
which contains an element of order  by the induction hypothesis, its pre-image in
by the induction hypothesis, its pre-image in  then has order divisible by
then has order divisible by  .
.
In fact, using this we can prove Sylow I+ using the class equation (and without using the structure theorem for finite abelian groups). The case is done same as above. Now let
is done same as above. Now let  . If
. If  is abelian then it contains element
is abelian then it contains element  of order
of order  and
and  has a subgroup of order
has a subgroup of order 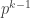 by the induction hypothesis and we take the preimage. If not then let
by the induction hypothesis and we take the preimage. If not then let  . If
. If  then
then  has a subgroup of order
has a subgroup of order 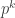 by the induction hypothesis. If
by the induction hypothesis. If 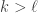 then
then  has a
has a  -Sylow subgroup
-Sylow subgroup  by the induction hypothesis and
by the induction hypothesis and  has a subgroup of order
has a subgroup of order  by the induction hypothesis and we take the pre-image again.
by the induction hypothesis and we take the pre-image again.
Finally, in the subproof 1 of Sylow III there should be twice instead of
instead of 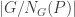 .
.
Thanks for the detailed comment! Re: Cauchy’s theorem, the argument I suggest doesn’t need the structure theorem for finite abelian groups; we only need to know that a finite abelian group of order is a module over
is a module over  , and then we can decompose into Sylow
, and then we can decompose into Sylow  -subgroups using the Chinese remainder theorem. But your inductive argument is even more elementary!
-subgroups using the Chinese remainder theorem. But your inductive argument is even more elementary!
That’s a nice proof of Sylow I+ as well. And yes, thanks for pointing out the typo.
I’ve revisited this after some time and I’ve just now realized that your CRT argument doesn’t work, unless I’m completely missing something. The CRT tells us that a finite abelian group is a direct sum of finite abelian groups with prime power exponents, but we don’t apriori know that these factors are -groups as you claim, right ? In fact that’s a special case of what we want to prove.
-groups as you claim, right ? In fact that’s a special case of what we want to prove.
Apologies for the very late response, I haven’t been thinking about math much lately. I’m not sure I understand the objection. A -group is a group all of whose elements have order a power of
-group is a group all of whose elements have order a power of  . If a finite group has exponent
. If a finite group has exponent 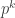 then all of its elements have order dividing
then all of its elements have order dividing 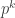 .
.
Maybe you meant to write “Sylow -subgroups” rather than
-subgroups” rather than  -groups? If we write a finite abelian group as a direct sum of finite abelian
-groups? If we write a finite abelian group as a direct sum of finite abelian  -groups for distinct primes
-groups for distinct primes  then it’s clear that each one has index coprime to
then it’s clear that each one has index coprime to  as needed for our definition of Sylow, since the index of each subgroup is just the product of the orders of the other subgroups.
as needed for our definition of Sylow, since the index of each subgroup is just the product of the orders of the other subgroups.
Sorry for the late answer as well. To clarify, in the previous comment by -group I meant a group of order a power of
-group I meant a group of order a power of  , I should have made that clear. Let me give a simple example. Let
, I should have made that clear. Let me give a simple example. Let  be an abelian group of order
be an abelian group of order 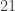 and
and  . Then the CRT tells us that
. Then the CRT tells us that  , where
, where  has exponent
has exponent 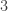 and
and  has exponent
has exponent 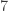 . Obviously if we knew that
. Obviously if we knew that  is non-trivial then we’d be done, however CRT alone doesn’t rule out the possibility
is non-trivial then we’d be done, however CRT alone doesn’t rule out the possibility  ,
,  , right ?
, right ?
Very nice! I loved the proof hidden in everything that p-groups are nilpotent using GL_n.
Two typos: In proof 1 of Cauchy’s theorem, you write floor of n^2/p, when you mean floor of n/p^2. Also in subproof 1 of Sylow III, both instances of G/N_G(P) should be N_G(P)/P.
Thanks! Fixed.