As a warm-up to the subject of this blog post, consider the problem of how to classify matrices
up to change of basis in both the source (
) and the target (
). In other words, the problem is to describe the equivalence classes of the equivalence relation on
matrices given by
.
It turns out that the equivalence class of is completely determined by its rank
. To prove this we construct some bases by induction. For starters, let
be a vector such that
; this is always possible unless
. Next, let
be a vector such that
is linearly independent of
; this is always possible unless
.
Continuing in this way, we construct vectors such that the vectors
are linearly independent, hence a basis of the column space of
. Next, we complete the
and
to bases of
in whatever manner we like. With respect to these bases,
takes a very simple form: we have
if
and otherwise
. Hence, in these bases,
is a block matrix where the top left block is an
identity matrix and the other blocks are zero.
Explicitly, this means we can write as a product
where has the block form above, the columns of
are the basis of
we found by completing
, and the columns of
are the basis of
we found by completing
. This decomposition can be computed by row and column reduction on
, where the row operations we perform give
and the column operations we perform give
.
Conceptually, the question we’ve asked is: what does a linear transformation between vector spaces “look like,” when we don’t restrict ourselves to picking a particular basis of
or
? The answer, stated in a basis-independent form, is the following. First, we can factor
as a composite
where is the image of
. Next, we can find direct sum decompositions
and
such that
is the projection of
onto its first factor and
is the inclusion of the first factor into
. Hence every linear transformation “looks like” a composite
of a projection onto a direct summand and an inclusion of a direct summand. So the only basis-independent information contained in is the dimension of the image
, or equivalently the rank of
. (It’s worth considering the analogous question for functions between sets, whose answer is a bit more complicated.)
The actual problem this blog post is about is more interesting: it is to classify matrices
up to orthogonal change of basis in both the source and the target. In other words, we now want to understand the equivalence classes of the equivalence relation given by
.
Conceptually, we’re now asking: what does a linear transformation between finite-dimensional Hilbert spaces “look like”?
Inventing singular value decomposition
As before, we’ll answer this question by picking bases with respect to which is as easy to understand as possible, only this time we need to deal with the additional restriction of choosing orthonormal bases. We will follow roughly the same inductive strategy as before. For starters, we would like to pick a unit vector
such that
; this is possible unless
is identically zero, in which case there’s not much to say. Now, there’s no guarantee that
will be a unit vector, but we can always use
as the beginning of an orthonormal basis of . The question remains which of the many possible values of
to use. In the previous argument it didn’t matter because they were all related by change of coordinates, but now it very much does because the length
may differ for different choices of
. A natural choice is to pick
so that
is as large as possible (hence equal to the operator norm
of
); writing
, we then have
.
is called the first singular value of
,
is called its first right singular vector, and
is called its first left singular vector. (The singular vectors aren’t unique in general, but we’ll ignore this for now.) To continue building orthonormal bases we need to find a unit vector
orthogonal to such that
is linearly independent of
; this is possible unless
, in which case we’re already done and
is completely describable as
; equivalently, in this case we have
.
We’ll pick using the same strategy as before: we want the value of
such that
is as large as possible. Note that since
, this is equivalent to finding the value of
such that
is as large as possible. Call this largest possible value
and write
.
At this point we are in trouble unless ; if this weren’t the case then our strategy would fail to actually build an orthonormal basis of
. Very importantly, this turns out to be the case.
Key lemma #1: Suppose is a unit vector maximizing
. Let
be a unit vector orthogonal to
. Then
is also orthogonal to
.
Proof. Consider the function
.
The vectors are all unit vectors since
are orthonormal, so by construction (of
) this function is maximized when
. In particular, its derivative at
is zero. On the other hand, we can expand
out using dot products as
.
Now we can compute the first-order Taylor series expansion of this function around , giving
so setting the first derivative equal to gives
as desired.
This is the technical heart of singular value decomposition, so it’s worth understanding in some detail. Michael Nielsen has a very nice interactive demo / explanation of this. Geometrically, the points trace out an ellipse centered at the origin, and by hypothesis
describes the semimajor axis of the ellipse: the point furthest away from the origin. As we move away from
, to first order we are moving slightly in the direction of
, and so if
were not orthogonal to
it would be possible to move slightly further away from the origin than
by moving either in the positive or negative
direction, depending on whether the angle between
and
is greater than or less than
. The only way to ensure that moving in the direction of
does not, to first order, get us further away from the origin is if
is orthogonal to
.
Note that this gives a proof that the semiminor axis of an ellipse – the point closest to the origin – is always orthogonal to its semimajor axis. We can think of key lemma #1 above as more or less being equivalent to this fact, also known as the principal axis theorem in the plane, and which is also closely related to but slightly weaker than the spectral theorem for real matrices.
Thanks to key lemma #1, we can continue our construction. With as before, we inductively produce orthonormal vectors
such that
is maximized subject to the condition that
for all
, and write
where is the maximum value of
on all vectors
orthogonal to
; note that this implies that
.
The are the singular values of
, the
are its right singular vectors, and the
are its left singular vectors. Repeated application of key lemma #1 shows that the
are an orthonormal basis of the column space of
, so the construction stops here:
is identically zero on the orthogonal complement of
, because if it weren’t then it would take a value orthogonal to
. This means we can write
as a sum
.
This is one version of the singular value decomposition (SVD for short) of , and it has the benefit of being as close to unique as possible. A more familiar version of SVD is obtained by completing the
and
to orthonormal bases of
and
(necessarily highly non-unique in general). With respect to these bases,
takes, similar to the warm-up, a block form where the top left block is the diagonal matrix with entries
and the remaining blocks are zero. Hence we can write
as a product
where has the above block form,
has columns given by
, and
has columns given by
.
So, stepping back a bit: what have we learned about what a linear transformation between Hilbert spaces looks like? Up to orthogonal change of basis, we’ve learned that they all look like “weighted projections”: we are almost projecting onto the image as in the warmup, except with weights given by the singular values
to account for changes in length. The only orthogonal-basis-independent information contained in a linear transformation turns out to be its singular values.
Looking for more analogies between singular value decomposition and the warmup, we might think of the singular values as a quantitative refinement of the rank, since there are of them where
is the rank, and if some of them are small then
is close (in the operator norm) to a linear transformation having lower rank.
Geometrically, one way to describe the answer provided by singular value decomposition to the question “what does a linear transformation look like” is that the key to understanding is to understand what it does to the unit sphere of
. The image of the unit sphere is an
-dimensional ellipsoid, and its principal axes have direction given by the left singular vectors
and lengths given by the singular values
. The right singular vectors
map to these.
Properties
Singular value decomposition has lots of useful properties, some of which we’ll prove here. First, note that taking the transpose of a singular value decomposition gives another singular value decomposition
showing that has the same singular values as
, but with the left and right singular vectors swapped. This can be proven more conceptually as follows.
Key lemma #2: Write . Then for every
, the left and right singular vectors
maximize the value of
subject to the constraint that
for all
, that
is orthogonal to
, and that
is orthogonal to
. This maximum value is
.
Proof. At the maximum value of subject to the constraint that
is orthogonal to
and
is orthogonal to
, it must also be the case that if we fix
then
takes its maximum value at
. But for fixed
,
uniquely takes its maximum value when
is proportional to
(if possible), hence must in fact be equal to
; moreover, this is always possible thanks to key lemma #1. So we are in fact maximizing
subject to the above constraints and we already know the solution is given by .
Left-right symmetry: Let be the singular values, left singular vectors, and right singular vectors of
as above. Then
are the singular values, left singular vectors, and right singular vectors of
. In particular,
.
Proof. Apply key lemma #2 to , and note that
is the same either way, just with the roles of
and
switched.
Singular = eigen: The left singular vectors are the eigenvectors of
corresponding to its nonzero eigenvalues, which are
. The right singular vectors
are the eigenvectors of
corresponding to its nonzero eigenvalues, which are also
.
Proof. We now know that and that
, hence
and
.
Hence are orthonormal eigenvectors of
respectively. Moreover, these matrices have rank at most (in fact exactly)
, so this exhausts all eigenvectors corresponding to nonzero eigenvalues.
This gives an alternative route to understanding singular value decomposition which comes from writing as
and then applying the spectral theorem to to diagonalize, but I think it’s worth knowing that there’s a route to singular value decomposition which is independent of the spectral theorem.
In addition to the above algebraic characterization of singular values, the singular values also admit the following variational characterization.
Variational characterizations of singular values (Courant, Fischer): We have
and
.
Proof. For the first characterization, any -dimensional subspace
intersects
nontrivially, hence contains a unit vector of the form
.
We compute that
and hence that
.
We conclude that every contains
such that
, hence
. Equality is obtained when
.
The second characterization is very similar. Any -dimensional subspace
intersects
nontrivially, hence contains a unit vector of the form
.
We compute that
and hence that
.
We conclude that every contains a vector
such that
, hence
. Equality is obtained when
.
The second variational characterization above can be used to prove the following important theorem.
Low rank approximation (Eckart, Young): If is the SVD of
, let
where
has diagonal entries
and all other entries zero. Then
is the closest matrix to
in operator norm with rank at most
; that is,
minimizes
subject to the constraint that
. This minimum value is
.
Proof. Suppose is a matrix of rank at most
. Let
be the nullspace of
, which by hypothesis has dimension at least
. By the second variational characterization above, this means that it contains a vector
such that
, and since
this gives
and hence that . Equality is obtained when
as defined above.
The variational characterizations can also be used to prove the following inequality relating the singular values of two matrices and of their sum, which can be thought of as a quantitative refinement of the observation that the rank of a sum of two matrices is at most the sum of their ranks.
Additive perturbation (Weyl): Let be
matrices with singular values
. Then
.
Proof. We want to bound in terms of the singular values of
and
. By the second variational characterization, we have
.
To give an upper bound on a minimum value of a function we just need to give an upper bound on some value that it takes. Let and
be the subspaces of
of dimensions
respectively which achieve the minimum values of
and
respectively, and let
be their intersection. This intersection has dimension at least
, and by construction
.
Since has dimension at least
, the above is an upper bound on the value of
for any
-dimensional subspace
, from which the conclusion follows.
The slightly curious off-by-one indexing in the above inequality can be understood as follows: if and
are both very small, this means that
and
are close to matrices of rank at most
and
respectively, and hence
is close to a matrix of rank at most
, hence
also ought to be small.
Setting in the additive perturbation inequality we deduce the following corollary.
Singular values are Lipschitz: The singular values, as functions on matrices, are uniformly Lipschitz with respect to the operator norm with Lipschitz constant : that is,
.
Proof. Apply additive perturbation twice with , first to get
(remembering that is the operator norm), and second to get
(remembering that ).
This is very much not the case with eigenvalues: a small perturbation of a square matrix can have a large effect on its eigenvalues. This is explained e.g. in in this blog post by Terence Tao, and is related to pseudospectra.
Setting , or equivalently
, in the additive perturbation inequality, we deduce the following corollary.
Interlacing: Suppose are matrices such that
. Then
.
Proof. Apply additive perturbation twice, first to get
and second to get
.
Interlacing gives us some control over what happens to the singular values under a low-rank perturbation (as opposed to a low-norm perturbation; a low-rank perturbation may have arbitrarily high norm, and vice versa). For example, we learn that if all of the singular values are clumped together, then a rank- perturbation will keep most of the singular values clumped together, except possibly for either the
largest or
smallest singular values. We can’t expect any control over these, since in the worst case a rank-
perturbation can make the
largest singular values arbitrarily large, or make the
smallest singular values arbitrarily small.
A particular special case of a low-rank perturbation is deleting a small number of rows or columns (note that a row or column which is entirely zero does not affect the singular values, so deleting a row or column is equivalent to setting all of its entries to zero), in which case the upper bound above can be tightened.
Cauchy interlacing: Suppose is a matrix and
is obtained from
by deleting at most
rows. Then
.
Proof. The lower bound follows from interlacing. The upper bound follows from the observation that we have for all
, then applying either variational characterization of the singular values.
Cauchy interlacing also applies to deleting columns, or combinations of rows and columns, because the singular values are unchanged by transposition. In particular, we learn that if is obtained from
by deleting either a single row or a single column, then the singular values of
interlace with the singular values of
, hence the name.
In particular, if all of the singular values of are clumped together then so are those of
, with no exceptions. Taking the contrapositive, if the singular values of
are spread out, then the singular values of
must be as well.
Three special cases
Three special cases of the general singular value decomposition are worth pointing out.
First, if has orthogonal columns, or equivalently if
is diagonal, then the singular values
are the lengths of its columns, we can take the right singular vectors to be the standard basis vectors
, and we can take the left singular vectors to be the unit rescalings of its columns. This means that we can take
to be the identity matrix, and in general suggests that
is a measure of the extent to which the columns of
fail to be orthogonal (with the caveat that
is not unique and so in general we would want to look at the
closest to
).
Second, if has orthogonal rows, or equivalently if
is diagonal, then the singular values
are the lengths of its rows, we can take the left singular vectors to be the standard basis vectors
, and we can take the right singular vectors to be the unit rescalings of its rows. This means that we can take
to be the identity matrix, and in general suggests that
is a measure of the extent to which the rows of
fail to be orthogonal (with the same caveat as above).
Finally, if is square and an orthogonal matrix, so that
, then the singular values
are all equal to
, and an arbitrary choice of either the left or the right singular vectors uniquely determines the other. This means that we can take
to be the identity matrix, and in general suggests that
is a measure of the extent to which
fails to be orthogonal. In fact it is possible to show that the closest orthogonal matrix to
is given by
, or in other words by replacing all of the singular values of
with
, so
is precisely the distance from to the nearest orthogonal matrix. This fact can be used to solve the orthogonal Procrustes problem.
In general, we should expect that the SVD of a matrix is relevant to answering any question about
whose answer is invariant under left and right multiplication by orthogonal matrices. This includes, for example, the question of low-rank approximations to
with respect to operator norm we answered above, since both rank and operator norm are invariant.
Btw. In the proof of interlacing, I don’t see the first displayed equality: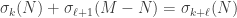 . What am I missing?
. What am I missing?
Oops, that’s a typo; it should just be on the RHS.
on the RHS.
Thanks for that concise and clear introduction to the SVD. I do not understand why it is often not even touched in a first class in linear algebra. It seems to me that it would make sense to introduce it even before the spectral theorem.
Regarding “weighted projections”: up to a scale factor (i.e., a single weight , you can view a linear transformation
, you can view a linear transformation
 between Euclidean spaces as an orthogonal projection.
between Euclidean spaces as an orthogonal projection.
Specifically, if and
and  are subspaces of
are subspaces of  of dimension
of dimension  and
and  respectively, and
respectively, and  is the orthogonal projection onto
is the orthogonal projection onto  restricted to
restricted to  , then, the singular values of
, then, the singular values of  are the cosines of the principal angles
are the cosines of the principal angles , then these singular values can take any value in $\latex [0,1]$.
, then these singular values can take any value in $\latex [0,1]$.
https://en.wikipedia.org/wiki/Angles_between_flats
If
So we see that any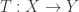 can be represented as
can be represented as  for an appropriate choice of $\latex X,Y$ as subspaces of
for an appropriate choice of $\latex X,Y$ as subspaces of  .
.
Also, regarding the best orthogonal transformation to represent , it is worth pointing out that you are talking about the orthogonal factor in the polar decomposition
, it is worth pointing out that you are talking about the orthogonal factor in the polar decomposition as a composition of an orthogonal matrix and a positive semidefinte matrix:
as a composition of an orthogonal matrix and a positive semidefinte matrix:
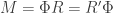 ,
,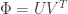 and $R= V \Sigma V^T$ and $R’ = U\Sigma U^T$.
and $R= V \Sigma V^T$ and $R’ = U\Sigma U^T$.
https://en.wikipedia.org/wiki/Polar_decomposition
which is an immediate consequence of the SVD. We can always represent our matrix
where
Thinking of the QR algorithm and the Toda lattice, you gain when you swap and refactor repeatedly as dressing transformations. Haven’t thought about what if anything reasonable happens when you permute the factors in a square SVD.