Group actions on categories

November 9, 2015 by Qiaochu Yuan

Yesterday we decided that it might be interesting to describe various categories as “fixed points” of Galois actions on various other categories, whatever that means: for example, perhaps real Lie algebras are the “fixed points” of a Galois action on complex Lie algebras. To formalize this we need a notion of group actions on categories and fixed points of such group actions.

So let $G$ be a group and $C$ be a category. For starters, we should probably ask for a functor $F(g) : C \to C$ for each $g \in G$ . Next, we might naively ask for an equality of functors

$\displaystyle F(g) F(h) = F(gh) : C \to C$

but this is too strict: functors themselves live in a category (of functors and natural transformations), and so we should instead ask for natural isomorphisms

$\displaystyle \eta(g, h) : F(g) F(h) \cong F(gh)$ .

These natural isomorphisms should further satisfy the following compatibility condition: there are two ways to use them to write down an isomorphism $F(g) F(h) F(k) \cong F(ghk)$ , and these should agree. More explicitly, the composite

$\displaystyle F(g) F(h) F(k) \xrightarrow{F(g) \eta(h, k)} F(g) F(hk) \xrightarrow{\eta(g, hk)} F(ghk)$

should be equal to the composite

$\displaystyle F(g) F(h) F(k) \xrightarrow{\eta(g, h) F(k)} F(gh) F(k) \xrightarrow{\eta(gh, k)} F(ghk)$ .

(There’s also some stuff going on with units which I believe we can ignore here. I think we can just require that $F(e) = \text{id}_C$ on the nose and nothing will go too horribly wrong.)

These natural isomorphisms $\eta(g, h)$ can be regarded as a natural generalization of 2-cocycles, and the condition above as a natural generalization of a cocycle condition. Below the fold we’ll describe this and other aspects of this definition in more detail, and we’ll end with two puzzles about the relationship between this story and group cohomology.

Why do this?

There are several ways to justify this definition. The basic justification is that categories themselves naturally live in a 2-category: accordingly, their endomorphisms $\text{End}(C)$ form monoidal categories, and we’ve written down above is precisely a (strong) monoidal functor from $G$ , regarded as a discrete monoidal category, to $\text{End}(C)$ . Said another way, the automorphisms $\text{Aut}(C)$ form not a group but a 2-group, and what we’ve written above is the definition of a morphism $G \to \text{Aut}(C)$ of 2-groups.

If we’d gone with the more naive definition, we would’ve ended up with a notion of groups acting on categories which wouldn’t have transported across equivalence of categories.

Where do 2-cocycles come into this?

Suppose that every $F(g)$ is the identity functor $\text{id}_C : C \to C$ . (Abstractly, this is a natural thing to do if every automorphism $C \to C$ is equivalent to the identity; then we can replace each $F(g)$ with the identity while changing the $\eta(g, h)$ appropriately.) Then each $\eta(g, h)$ is a natural isomorphism $\text{id}_C \to \text{id}_C$ , or equivalently an element of the group of units $Z(C)^{\times}$ of the center $Z(C)$ , and the compatibility condition becomes

$\displaystyle \eta(g, hk) \eta(h, k) = \eta(gh, k) \eta(g, h) \in Z(C)^{\times}$ .

Hence, in this special case, the $\eta$ precisely describe a 2-cocycle with coefficients in $Z(C)^{\times}$ .

What about cohomology?

The point of 2-cocycles is that they can be used to describe second group cohomology; where does that come into the picture?

Abstractly, second group cohomology $H^2(BG, A)$ can be described as homotopy classes of maps $BG \to B^2 A$ , where $BG$ is the classifying space of $G$ and $B^2 A$ is the classifying space of the classifying space of $A$ , or equivalently the Eilenberg-MacLane space $K(A, 2)$ . These are the same as homotopy classes of maps $G \to BA$ of 2-groups (by the homotopy hypothesis), and if the 2-group $\text{Aut}(C)$ is connected in the sense that $\pi_0(\text{Aut}(C)) = 1$ (which, as above, is precisely the condition that every automorphism $C \to C$ is equivalent to the identity), then

$\displaystyle \text{Aut}(C) \cong B Z(C)^{\times}$

as 2-groups, and hence in this special case actions of $G$ on $C$ are classified by group cohomology $H^2(BG, Z(C)^{\times})$ with coefficient in the group of units of the center of $C$ . In general, maps of 2-groups $G \to \text{Aut}(C)$ can be thought of as “nonabelian group cohomology,” with coefficients in a 2-group.

Concretely, let’s write down what it ought to mean for two group actions $(F_1, \eta_1), (F_2, \eta_2)$ to be equivalent. For starters, we should probably ask for a family of natural isomorphisms

$\displaystyle \alpha(g) : F_1(g) \cong F_2(g)$

and next we should ask for some compatibility between these isomorphisms and the “2-cocycles” $\eta_1, \eta_2$ . The natural compatibility to ask for is that the composites

$\displaystyle F_1(g) F_1(h) \xrightarrow{\eta_1(g, h)} F_1(gh) \xrightarrow{\alpha(gh)} F_2(gh)$

and

$\displaystyle F_1(g) F_1(h) \xrightarrow{\alpha(g) \alpha(h)} F_2(g) F_2(h) \xrightarrow{\eta_2(g, h)} F_2(gh)$

are equal. In the special case where all of the $F_1(g), F_2(g)$ are equal to the identity $\text{id}_C$ , the isomorphisms $\alpha(g)$ again take values in $Z(C)^{\times}$ , and the compatibility above becomes

$\displaystyle \alpha(gh) \eta_1(g, h) = \eta_2(g, h) \alpha(g) \alpha(h)$

which, with a little rearranging (using the fact that $Z(C)^{\times}$ is abelian), becomes

$\displaystyle \frac{\eta_1(g, h)}{\eta_2(g, h)} = \frac{\alpha(g) \alpha(h)}{\alpha(gh)}$ .

This means precisely that the 2-cocycles $\eta_1$ and $\eta_2$ differ by a 2-coboundary in the usual sense.

Okay, but do you have any interesting examples?

Let $C = \text{Mod}(k)$ be the category of vector spaces over a field $k$ . Every automorphism of $C$ as a $k$ -linear category turns out to be equivalent to the identity. (Without the $k$ -linearity condition, any automorphism of $k$ induces an automorphism of $C$ .) The center $Z(C)$ is $k$ itself, so its group of units is $k^{\times}$ . Hence the set of isomorphism classes of actions of a group $G$ on $C$ can be identified with the cohomology group

$\displaystyle H^2(BG, k^{\times})$ .

Puzzle 1: This cohomology group also appears when classifying projective representations of $G$ over $k$ . Is this a coincidence?

Puzzle 2: In terms of the description above as the set of isomorphism classes of actions, where does the group structure on this set come from, and why is it abelian?

Posted in math.CT, math.GR | Tagged 2-categories, cohomology, MaBloWriMo | 13 Comments

13 Responses

on May 31, 2016 at 11:03 am | Reply Higher linear algebra | Annoying Precision

[…] where groups (or higher versions of groups, such as 2-groups) act on higher vector spaces. Previously we saw such actions occur naturally in Galois descent: namely, if is a Galois extension with […]
on November 16, 2015 at 7:55 pm | Reply Stating Galois descent | Annoying Precision

[…] of functors (where again we’re taking compositions in diagrammatic order) satisfying the usual cocycle condition that the two natural isomorphisms we can write down from this data agree. We’ll also want unit isomorphisms satisfying the same compatibility as before. This is just spelling out the definition of a 2-functor from the category of separable extensions of to the 2-category , and in particular each naturally acquires an action of (where we mean automorphisms of extensions of , hence if is Galois this is the Galois group) in precisely the sense we described earlier. […]
on November 13, 2015 at 6:10 pm | Reply Projective representations give categorical representations | Annoying Precision

[…] us to match up the 2-cocycles that are about to appear with the 2-cocycles that appeared when we classified -linear actions of on . Apart from this observation we will no longer need to explicitly talk about the Morita […]
on November 12, 2015 at 7:29 pm | Reply Projective representations | Annoying Precision

[…] Three days ago we stated the following puzzle: we can compute that isomorphism classes of -linear actions of a group on the category of vector spaces over a field correspond to elements of the cohomology group […]
on November 11, 2015 at 8:17 pm | Reply Fixed points of group actions on categories | Annoying Precision

[…] Previously we described what it means for a group to act on a category (although we needed to slightly correct our initial definition). Today, as the next step in our attempt to understand Galois descent, we’ll describe what the fixed points of such a group action are. […]
on November 10, 2015 at 8:25 pm | Reply Units | Annoying Precision

[…] « Group actions on categories […]
on November 10, 2015 at 4:44 am | Reply sure

Just some little question about your definition of group acting on a category. The (should I say one?) “good” definition of a group acting on something is given by models of the sketch of a group action into the category you consider (product preserving functors from the sketch of group to the category you’re interested in). You can always take a model of your sketch of a group action in Cat. If you do so, you would have a group-object in Cat acting (in the usual sense) on a category. Why isn’t such definition good for your purposes?
- on November 10, 2015 at 11:23 am | Reply Qiaochu Yuan
  
  Because Cat isn’t a category, it’s a 2-category, and the correct definition takes this extra structure into account. The naive definition doesn’t, for example, transport across an equivalence of categories; that is, if you have a group $G$ acting on a category $C$ in the naive sense, and you also have an equivalence of categories $C \cong C'$ , then you do not get a group action in the naive sense on $C'$ .
  - on November 10, 2015 at 1:04 pm | Reply sure
    
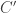    Regardless of the strictness concerns, I’m not even sure that the definition I propose is equivalent to your when the “group object” is supported over a category with 1 object.
    - on November 10, 2015 at 1:19 pm | Reply Qiaochu Yuan
      
      That’s correct, it’s not, and this distinction is important.
on November 10, 2015 at 12:20 am | Reply Zhen Lin

You can require $F (\mathrm{id}) = \mathrm{id}$ if you want, but I think there is still a compatibility condition: we should require that the composite $F (h) \cong \mathrm{id} \circ F (h) = F (\mathrm{id}) \circ F (h) \cong F (\mathrm{id} \circ h)$ be equal to the image of the left unitor $h \cong \mathrm{id} \circ F$ , and similarly for the right unitor. 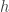(Here, $F$ is a pseudofunctor between bicategories.) In your case, this amounts to the condition that $\eta (g, h)$ be the identity when either $g$ or $h$ is the identity.

Curiously, there is Simpson’s conjecture, which says something to the effect that you can strictify everything except units.
- on November 10, 2015 at 11:10 am | Reply Qiaochu Yuan
  
  Hmm, yeah, in fact I’ve been careless. I neglected the difference between maps of spaces and maps of based spaces…
- on November 10, 2015 at 8:26 pm | Reply Qiaochu Yuan
  
  Hang on, no, basepoints aren’t the problem. I should just write something about units to be safe.

Comments RSS

	ZW on The double commutant theo…
	auto on More about the Schrödinger equ…
	Jaromir Kuben on Meditation on the Sylow theore…
	Qiaochu Yuan on Meditation on the Sylow theore…
	Qiaochu Yuan on Some remarks on the infinitude…

Annoying Precision

"A good stock of examples, as large as possible, is indispensable for a thorough understanding of any concept, and when I want to learn something new, I make it my first job to build one." – Paul Halmos