The problem of finding solutions to Diophantine equations can be recast in the following abstract form. Let be a commutative ring, which in the most classical case might be a number field like
or the ring of integers in a number field like
. Suppose we want to find solutions, over
, of a system of polynomial equations
.
Then it’s not hard to see that this problem is equivalent to the problem of finding -algebra homomorphisms from
to
. This is equivalent to the problem of finding left inverses to the morphism
of commutative rings making an
-algebra, or more geometrically equivalent to the problem of finding right inverses, or sections, of the corresponding map
of affine schemes. Allowing to be a more general scheme over
can also capture more general Diophantine problems.
The problem of finding sections of a morphism – call it the section problem – is a problem that can be stated in any category, and the goal of this post is to say some things about the corresponding problem for spaces. That is, rather than try to find sections of a map between affine schemes, we’ll try to find sections of a map between spaces; this amounts, very roughly speaking, to solving a “topological Diophantine equation.” The notation here is meant to evoke a particularly interesting special case, namely that of fiber bundles.
We’ll try to justify the section problem for spaces both as an interesting problem in and of itself, capable of encoding many other nontrivial problems in topology, and as a possible source of intuition about Diophantine equations. In particular we’ll discuss what might qualify as topological analogues of the Hasse principle and the Brauer-Manin obstruction.
Preliminaries: morphisms as families
It will be useful to keep the following intuition in mind throughout this post: in a category of some sort of spaces, a morphism should be thought of as a family or bundle of spaces
varying over the base space
, and anything one does for spaces one can try to do for families of spaces. Here by
I mean a suitable pullback, namely the pullback of a diagram of the form
, where
is any object in the category in question serving as a point. From this perspective, trying to find a section
of
can be thought of as finding a “continuous” choice of point
in each space in this family: it can be thought of as the families version of the problem of finding a point in a space.
This is Grothendieck’s relative point of view, which was perhaps first made famous via the Grothendieck-Riemann-Roch theorem in algebraic geometry. This is the families version of the Hirzebruch-Riemann-Roch theorem. But there are simpler examples of the relative point of view.
Example. A covering map should be thought of as a locally constant family of sets
varying over
. This idea can be made precise as the following restatement of the classification of covering spaces: for reasonable base spaces
(locally contractible should be enough; there’s no need to require that
or its covers be path-connected), there is an equivalence of categories between
- covering spaces of
and covering maps, and
- functors
from the fundamental groupoid of
to
and natural transformations
where the equivalence is given in one direction by monodromy: we send a covering space to the functor sending a point
to the fiber
and we send a path
between points to map of sets
given by taking the unique lift
of
to a path in
starting at a point in
and then evaluating it at
to obtain a point in
.
This expanded version of the classification of covering spaces, where we do not restrict to path-connected bases or path-connected covers, results in a category with much better formal properties than the category of path-connected covers of a path-connected base; for example, we can now take coproducts and products of covering spaces, which correspond to taking disjoint unions and fiber products respectively. In fact, the equivalence above makes it clear that anything we can do to a family of sets we can do fiberwise to a family of covering spaces.
(This is a good place to really see fiber products earn their names: thinking of a morphism in terms of its fibers
makes it clear that taking the fiber product of two such morphisms
amounts, on fibers, to literally taking the products of the fibers, thanks to the fact that limits commute with limits.)
Preliminaries: the function field analogy
The analogy we’re implicitly trying to make here can be thought of as a relative of the function field analogy. Already it’s interesting to think about the function field analogue of solving Diophantine equations, e.g. finding solutions in to systems of polynomial equations with coefficients in
, where
is a field. Geometrically such a thing defines a map
which, from the relative point of view, we should think of as a family of affine varieties over the affine line, and finding a solution to the corresponding Diophantine equation amounts to “continuously” choosing a point in each of these varieties. When , we can even equip the corresponding complex affine varieties with their analytic topologies, and then ask for topological obstructions for the corresponding map of topological spaces to admit a continuous section; such obstructions also obstruct the original map of varieties having an algebraic section.
Example. Sections of the map
encode solutions to the Diophantine equation , where we want to find solutions
. This equation of course fails to have a solution, but it fails to have a solution for several reasons which generalize to more complicated situations.
First, the fiber over each -point
of the affine line is the affine scheme
whose points over
are the solutions to
in
, so if there are any
with no square roots then there is a local obstruction to the existence of a solution to
in
. In more number-theoretic language, an obstruction to the existence of a solution is the existence of a solution
.
But this is not enough: even if is algebraically closed, there are still no solutions. There is a further problem that
is necessarily divisible by
an even number of times, while
is divisible by
once (which is odd). Equivalently, the problem is that there is no solution
, or more geometrically, that the map above, which can equivalently be described as the squaring map
,
fails to be surjective on Zariski tangent spaces at . Yet another description of the problem is that although there exists a solution locally at
, that local solution cannot be extended to a formal neighborhood of
.
Moreover, even if we delete by localizing away from it to get a map
then there is still no section / solution. One way to describe the problem is that although we can no longer talk about solutions , we can still talk about solutions in formal Laurent series
in
, and looking at
-adic valuations we see that there aren’t any such solutions. Equivalently, we are looking at solutions in a formal neighborhood of the deleted point even though we can no longer look at the deleted point itself.
There is a related global topological obstruction in the case that , which is that we get an induced map on the punctured complex line
which induces multiplication by on
, and this map has no section (in particular, is not surjective) so the original map cannot either.
Examples: associated bundles of vector bundles
In this section we’ll describe a large source of interesting examples of section problems in topology coming from vector bundles.
Let be a vector bundle on a base
, for example the tangent bundle of a smooth manifold. From
we can construct various associated bundles whose sections, if they exist, have interesting meanings in terms of
. (The problem of classifying sections of
itself is also interesting, but the problem of determining whether they exist is not, since the zero section always exists.)
Example. If denotes the fiber over
, then removing the zero section from
gives a bundle over
whose fiber over
is
and whose sections are precisely nonvanishing sections of
. More generally, there is an associated bundle whose fiber over
is linearly independent
-tuples
and whose sections are precisely
-tuples of (pointwise) linearly independent sections of
. Already the problem of describing the largest
for which this is possible for the tangent bundles of spheres is an extremely interesting problem, solved by Adams in 1962 using topological K-theory. For example, the only spheres
for which it is possible to construct the maximum possible number of linearly independent vector fields, namely
, occur when
; they can be constructed using the fact that these are precisely the unit spheres in the complex numbers, the quaternions, and the octonions respectively.
Characteristic classes give obstructions to finding such sections: using the fact that the total Stiefel-Whitney resp. Chern class is multiplicative under direct sum, it’s not hard to show that if a real resp. complex vector bundle of dimension
admits
linearly independent sections then its
top Stiefel-Whitney classes
resp. Chern classes
vanish. Similarly, if
is a real oriented vector bundle and it admits a single nonvanishing section then its Euler class vanishes.
Subexample. For the tangent bundles of oriented smooth closed manifolds, where the Euler class evaluates to the Euler characteristic, the last observation above reproduces the Poincaré–Hopf theorem and shows that the even-dimensional spheres don’t admit nonvanishing vector fields. Applied to
, we reproduce the hairy ball theorem.
Example. If is a real vector bundle of even dimension
, then there is an associated bundle whose fiber over
is the space of complex structures on
(that is, the space of ways to equip
with the structure of a complex vector space). Explicitly, this is the space of automorphisms
such that
, topologized as a subspace of
with the usual Euclidean topology.
acts transitively on the space of complex structures on
, with the stabilizer of a fixed complex structure (coming from a fixed identification
isomorphic to
. Similar remarks apply in the presence of a Riemannian metric on
and hence the space of complex structures can be identified as a homogeneous space
.
Sections of the corresponding bundle then correspond, unsurprisingly, to complex structures on (that is, ways to equip
with the structure of an
-dimensional complex vector bundle). When
is the tangent bundle of
, equipping
with a complex structure is in turn an obstruction to equipping
with the structure of a complex manifold; a manifold which has the weaker structure of a complex structure on its tangent bundle is called an almost complex manifold, and the distinction between the two is given by the Newlander-Nirenberg theorem.
Characteristic classes also give obstructions to finding complex structures: as we saw earlier, if a real vector bundle has a complex structure then the odd Stiefel-Whitney classes
vanish and the even Stiefel-Whitney classes
are reductions of Chern classes
; equivalently, after applying the Bockstein homomorphism
, the odd integral Stiefel-Whitney classes
vanish. The Pontryagin classes must also satisfy some identities determining them in terms of Chern classes.
Moreover, since any symplectic manifold admits a compatible almost complex structure, any obstruction to having an almost complex structure is also an obstruction to having a symplectic structure.
Subexample. This is another problem that is already interesting for spheres. First, using Pontryagin classes we can show that the spheres don’t admit almost complex structures, as follows. If
admitted an almost complex structure, then it would have Chern classes, although all of them except
automatically vanish. This last Chern class does not vanish since it must be equal to the Euler characteristic
, where we identify
via an orientation. We know that we can express the Pontryagin classes of a complex vector bundle in terms of its Chern classes, and here that gives us a top Pontryagin class of
.
On the other hand, since all spheres are stably parallelizable, all of their Pontryagin classes must vanish; contradiction.
Next, an argument relying on stronger tools in fact shows that doesn’t admit an almost complex structure for
. Namely, the following version of the Hirzebruch-Riemann-Roch theorem can be deduced from the Atiyah-Singer index theorem: if
is a closed almost complex manifold and
is a complex vector bundle on
, then
is the index of a certain Dirac operator, and hence is an integer. Here is the Chern character of
while
denotes the Todd class. If
admits an almost complex structure, then
and
are nonvanishing only in bottom and top degrees, since in all other degrees the relevant cohomology groups vanish, and so the above expression reduces to
where and
denote the components of the Chern character and Todd class respectively in
. Applying the index theorem twice, first with
a trivial bundle, we conclude that the Todd genus
is an integer and hence that
for all complex vector bundles . Now taking
to be the tangent bundle of
itself, and using the fact that we know that all of the Chern classes vanish except the top class
, which as above must be twice a generator of
, we compute (e.g. using the splitting principle) that
and hence that
from which it follows that , so
as desired.
In fact the intermediate result above, that for a -dimensional complex vector bundle
on
the top Chern class
is divisible by
, is true for all
and is due to Bott; see this blog post by Akhil Mathew for an alternate proof using K-theory. The proof above can be salvaged using a stronger version of the Hirzebruch-Riemann-Roch theorem: it suffices for
to have a
-structure, which unlike an almost complex structure every sphere possesses.
Since odd-dimensional manifolds can’t admit almost complex structures, the only spheres we haven’t ruled out at this point are and
.
has a complex structure coming from its identification with the complex projective line
, while
has an almost complex structure coming from its identification with the unit imaginary octonions. It is a major open problem to determine whether
admits a complex structure; see, for example, this MO question.
Some categorical remarks
Recall that if a morphism has a section, or equivalently a right inverse, then it is called a split epimorphism, and in particular it is an epimorphism. Recall also the following two equivalent alternative definitions of a split epimorphism:
- A split epimorphism is a morphism
which is an absolute epimorphism in the sense that if
is any functor, then
is an epimorphism;
- A split epimorphism is a morphism
which is surjective on generalized points in the sense that for any other object
, the induced map
is surjective.
Another way of restating the second definition which is particularly amenable to topological thinking is that a split epimorphism is a map such that any map
lifts to a map
along
.
Both of these equivalent definitions give several straightforward obstructions for a map of spaces to admit a section. For example, applying homology functors, we get that the induced maps
on homology must admit sections: this happens iff
is surjective and the short exact sequence
splits. Similarly, the induced maps on fundamental groups (with some choice of basepoint) must admit sections, and again this happens iff
is surjective and the short exact sequence
splits. If is a smooth map between smooth manifolds, then
must be a submersion. And so forth.
Two Hasse principles
In this section the term “Hasse principle” will mean a necessary condition for a section to exist which is roughly of the form “in order for a section to exist, it must exist locally,” analogous to the statement that in order for a Diophantine equation to have a solution over it must have a solution over all completions
. The term “Hasse principle holds” means the stronger statement that this condition is also sufficient, which won’t hold for most of our examples (much as the condition in the Hasse principle itself isn’t sufficient for most Diophantine equations).
The simplest thing that could be called a topological Hasse principle is the pointwise Hasse principle: in order for a map to have a section
, the fiber
over every point
must be nonempty, since
for all
. Equivalently,
must be surjective. Intuitively, for a section to exist, it must first exist locally in the most local possible sense, namely pointwise. The number-theoretic analogue is that in order for a Diophantine equation with integer coefficients to have solutions over
it must have solutions over
for all
.
The pointwise Hasse principle is very weak. Its hypothesis is always satisfied for fiber bundles, and in particular is always satisfied for covering maps. But a nontrivial covering map (say path-connected, with a path-connected base) never has a section because the induced map
on fundamental groups is not surjective with any choice of basepoints, and so cannot have a section.
(Note, however, that “a map of sets has a section iff it’s surjective” is equivalent to the axiom of choice, and hence we can think of the axiom of choice as asserting that the pointwise Hasse principle holds for sets.)
But there are even simpler examples involving no algebraic topology: consider the map
where denotes the disjoint union and so there are two copies of
in the codomain, and where
restricts to the obvious inclusion on each connected component of the codomain. This map has no section despite the fact that the base is contractible and the induced map on
is surjective, so no homotopy-invariant argument can detect this fact.
In the above example not only fails to have a section defined on all of
, but in fact it fails to have a section defined on any neighborhood of
. This suggests the following construction. Starting from a map
we can build a sheaf
on
whose sections over an open subset
(in the sheaf sense) consist of sections of
(in the right-inverse sense) over
:
.
The problem of finding a section of is then equivalent to the problem of finding a global section
of the sheaf
. This sheaf is a convenient way of encoding the local-to-global aspects of this problem.
does not allow us to recover the data of the fibers
of
. The next best thing we can do is to look at the stalks at each point
, defined as a cofiltered limit
over for all
containing
. Equivalently,
consists of equivalence classes of sections of
over an open neighborhood of
modulo the equivalence relation of being equal in some possibly smaller open neighborhood of
; these are the germs of sections of
at
.
Looking at stalks gives us a stalkwise Hasse principle: in order for to have a section, each stalk
must be non-empty. Equivalently, for every
there must be a section of
defined on some open neighborhood of
. A number-theoretic analogue is looking at solutions over the
-adics rather than just looking at solutions
(although this involves looking at formal neighborhoods rather than, say, open neighborhoods in the Zariski topology), so we’re getting closer to the actual Hasse principle.
The stalkwise Hasse principle successfully detects that the map
has no section, since the stalk at is empty: equivalently,
has no section defined in a neighborhood of
. But a slight modification of this example defeats even the stalkwise Hasse principle: consider now the map
.
Here the problem is that there is a unique section over , and similarly a unique section over
, but these two sections don’t agree on their intersection
. And again the base is contractible.
Like the pointwise Hasse principle, the hypothesis of the stalkwise Hasse principle is also satisfied for all fiber bundles. So even in fairly straightforward examples we see that there are many global obstructions for sections to exist. In that light the fact that the usual Hasse principle holds for quadratic forms is quite surprising.
A Brauer-Manin obstruction
Suppose that is a map and
is an open cover of the base for which we’ve found, on each open
, a local section
. (This is equivalent to the hypothesis of the stalkwise Hasse principle.) Then to check whether the
glue to a section
it remains to check whether they agree on intersections in the sense that
where .
Now suppose that for whatever reason we don’t want to or can’t do this, but that we understand the cohomology of all of the spaces involved fairly well. Then we can do the following instead: each induces a map
which gives us a pairing
from which we can build a pairing
.
In other words, given a family of local sections, we can pull a cohomology class in
back along all of the local sections to get a family of cohomology classes in
. But there are restrictions on what families of cohomology classes we can get in this way: if
is a global section, then it induces a map
which lets us construct a pairing
and this pairing and the above pairing fit into a commutative square
expressing the following restriction: if the glue together to (equivalently, are induced by restriction from) a global section
, then pairing the
with a cohomology class in
gives a family of cohomology classes in
which glue together to (equivalently, are induced by restriction from) a cohomology class in
. In other words, there is a pairing
and a necessary condition for a family of local sections to glue to a global section
is that the family must pair to zero with every class in
.
This is what might be called a topological Brauer-Manin obstruction. The number-theoretic analogue, namely the usual Brauer-Manin obsruction, comes from making the following substitutions to the above picture.
First, is
(for simplicity),
is a variety over
(for example, a smooth projective algebraic curve defined by equations with rational coefficients), and the
are
where
runs over all primes, including the “infinite prime”
, where
. So the situation is that we want to find rational points on the variety
, we’ve found points over
for all primes
, and we’d like to write down a cohomological obstruction to them gluing together to a rational point.
Next, is the Brauer group
of a scheme
; for
this is the Brauer group of
in the usual sense, and is equivalently the Galois cohomology group
or the etale cohomology group
.
In general the Brauer group is some torsion subgroup of . In particular,
, like
, is a contravariant functor in
.
This wouldn’t be a useful thing to write down if we didn’t know the Brauer groups of the relevant fields, but in fact we do (this is part of class field theory): are the Brauer groups
, which are equal to
when
is finite and
when
, and
is the Brauer group
, which fits into a short exact sequence
.
(In particular, the pullback of an element of to
is nontrivial for only finitely many primes
.) Letting
denote the
-points of the variety
, the number-theoretic analogue of the pairing we constructed above is a pairing
and the Brauer-Manin obstruction is the necessary condition for a collection of points in to lift to a point in
that this pairing must be zero for every element of
. I am told that there are examples of curves for which each
is non-empty but where the Brauer-Manin obstruction does not vanish, and examples of higher-dimensional varieties for which each
is non-empty and the Brauer-Manin obstruction vanishes but there are still no rational points.

You might be interested that the Brauer Manin obstruction can indeed be re-defined using (e’tale) homotopy theory, for details see my paper with y.Harpaz
Click to access 1110.0164v1.pdf
Nice Post…Detailed insights on Diophantine equations
Dear qiaochu,
I think one of $f_i$s in the line 5, must be constantly zero. Because the solution of the equational system needs to vanish all the ideal of generated by $f_i$s.
Aha, yes, that was a typo. Thanks!
There are examples of failure of Braur-Manin (due to Skorbogatov and later with an explanation by Poonen). The most recent strengthening of the Braur-Manin construction is by T. Schlank, and it is truly inspired by algebraic topology (namely, changing fixed points to homotopy fixed points).
Qiaochu,
As I believe you are alluding to with the statement “some torsion subgroup”, it’s an open question as to when (defined in terms of Azumaya algebras), which is the definition I believe you’re taking, is equal to
(defined in terms of Azumaya algebras), which is the definition I believe you’re taking, is equal to  . Is there some way in which your analogy makes this a reasonable thing to expect?
. Is there some way in which your analogy makes this a reasonable thing to expect?
Also, and I apologize if I missed it, you didn’t seem to mention that you can think of as being a colimit of
as being a colimit of  . This has obvious interpretations, topologically, in terms of
. This has obvious interpretations, topologically, in terms of 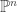 -bundles which are not the projectivization of vector bundles (I believe). This seems too apropos for there not to be a conection.
-bundles which are not the projectivization of vector bundles (I believe). This seems too apropos for there not to be a conection.
Thanks!
Oops–I made a typo. It should have said “in terms of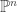 -bundles **up** to projectivizations of vector bundles”. Sorry!
-bundles **up** to projectivizations of vector bundles”. Sorry!
The analogy suggests (to me, anyway) that if this is a hard question then is the wrong invariant to look at, and we should instead be figuring out what is being represented by all of (or the entire torsion subgroup of)
is the wrong invariant to look at, and we should instead be figuring out what is being represented by all of (or the entire torsion subgroup of) 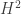 . I think this is done in a paper of Toen.
. I think this is done in a paper of Toen.
As for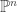 -bundles, one way to think about the Brauer class represented by such a bundle is as a characteristic class.
-bundles, one way to think about the Brauer class represented by such a bundle is as a characteristic class.