The goal of this post is to compute the cohomology of the -torus
in as many ways as I can think of. Below, if no coefficient ring is specified then the coefficient ring is
by default. At the end we will interpret this computation in terms of cohomology operations.
Method 1: Mayer-Vietoris
For this particular method write . We can compute the cohomology of
inductively by regarding it as the union of two copies of
with intersection
and using Mayer-Vietoris. The cohomological version of Mayer-Vietoris is a long exact sequence of the form
.
The maps are induced by pulling back along the inclusion
, whereas the maps
are induced by the difference between the pullbacks along the inclusions
. Because these maps are homotopic to the identity map
, we can think of
as being given by
where , and we can think of
as being given by two copies of a single map
, which we’ll denote by
. It follows that
is the antidiagonal copy
of
in
, hence
factors through the map
from
to
and
contains a copy of
given by
.
It also follows that is the diagonal copy
of
, hence that
is surjective. Finally,
is the kernel of
, hence the quotient of
by
is
. In other words, we have short exact sequences
.
But inductively it will turn out that all the groups involved are free abelian so all of these exact sequences split. In fact, inducting on the above relation it follows that the Poincaré polynomials
satisfy and
, hence
.
So by induction we conclude that . Note that we have not computed the cup product structure.
Method 2: the Künneth formula
This method will compute the cup product structure. is the product of
copies of
, whose cohomology as a ring is
; there are no interesting cup products. By the Künneth formula, the cohomology of
is the graded tensor product, as algebras, of
copies of
(since all of the cohomology groups involved are free). This is precisely the exterior algebra
, with each generator in degree
. In particular,
naturally, and under this isomorphism the cup product corresponds to the wedge product.
Method 3: de Rham cohomology
This method will compute the cohomology over by computing the de Rham cohomology of
. One particularly nice way to do this is to use the following.
Theorem: Let be a compact connected Lie group acting on a smooth manifold
. The inclusion
of invariant differential forms into differential forms is a quasi-isomorphism (induces an isomorphism on cohomology).
The idea behind this result is that, since is compact, there is an averaging operator
given by averaging over the action of
with respect to normalized Haar measure on
. But since
is connected, the action of any individual element of
is homotopic to the identity, so this average is also homotopic to the identity.
In particular, letting act on itself by translation, we conclude that we can compute its de Rham cohomology using translationally invariant differential forms on
, or equivalently on its universal cover
. But these are precisely the differential forms obtained by wedging together the
-forms
. The exterior derivative vanishes on all such forms, so we conclude that the de Rham cohomology of
is the exterior algebra on
.
Method 4: Hopf algebras
This method will compute the cohomology over . Since
is a topological group, it’s equipped with a product operation
. The induced map in cohomology has the form
by the Künneth formula. This map is coassociative and compatible with cup product, so equips with the structure of a bialgebra. Together with the map induced by the inversion map
and the identity
, the cohomology of
acquires the structure of a Hopf algebra, and in fact this was Hopf’s motivation for introducing Hopf algebras. Hopf algebras arising in this way satisfy the following very stringent structure theorem.
Theorem (Hopf): Let be a finite-dimensional graded commutative and cocommutative Hopf algebra over a field
of characteristic zero such that
(the Hopf algebra is connected). Then
is the exterior algebra on a finite collection of generators of odd degrees.
The comultiplication sends each generator to
, the antipode sends each generator
to
, and the counit sends each generator
to
.
To compute the cohomology of it therefore suffices to determine what the possible generators of the exterior algebra
are. For starters, let’s write
more abstractly as
where
is a finite-dimensional real vector space of dimension
and
is a lattice in
of full rank (the subgroup generated by a basis of
). Covering space theory gives us that
. By the Hurewicz theorem,
, so by the universal coefficient theorem,
.
This gives us generators of degree
, one for each element of a basis of
, and so
at the very least contains the exterior algebra
. But now we’re done: the cohomology can’t contain any generators of higher degree because wedging them with the
generators we’ve already found would produce nonzero elements of the cohomology of
in degrees higher than
, and no such elements exist (either because
admits a CW-decomposition involving cells of dimension at most
or because the de Rham complex only extends up to dimension
for a smooth manifold of dimension
).
Method 5: suspension
Recall that cohomology is a stable invariant in the sense that
where is the (reduced) suspension of
(here a pointed space). Recall also that for nice pointed spaces the suspension of a product has homotopy type
where is the wedge sum and
is the smash product. Finally, recall that
and that
, so
.
Two spaces are said to be stably homotopy equivalent if
for some
; in particular, stably homotopy equivalent spaces have isomorphic cohomology. The above result tells us that
is stably homotopy equivalent to
(once we know that suspension commutes with wedge sums). More generally, by induction we conclude that a product
is stably homotopy equivalent to a wedge obtained formally by expanding
,
where denotes the unit of the smash product, and removing the unit. It follows that
is stably homotopy equivalent to a wedge of
copies of the
-sphere,
, and by a simple application of Mayer-Vietoris (for wedge sums), the cohomology of such a wedge is the same as what we’ve computed before.
This argument does not get us the cup product structure, since the cup product is an unstable phenomenon; after suspension, all cup products are trivial. However, it does describe the stable homotopy type of , which contains information that cohomology doesn’t (e.g. about stable homotopy groups).
Method 6: cellular homology
To compute the cohomology of it suffices to compute the homology and apply either universal coefficients or Poincaré duality. It is possible to describe fairly concretely what the homology of
looks like using cellular homology. Recall that cellular homology describes a chain complex
computing the homology of a CW-complex which in degree
is free abelian on the
-cells in a cell decomposition of
. Our particular
admits a cell decomposition with
cells of dimension
given by starting with the minimal cell decomposition of
into two cells (a
-cell and a
-cell connecting the
-cell to itself) and taking products, where we’re thinking of cubical
-cells
here. Equivalently, we can think of
as being
with opposite
-faces identified, and then our cells are the faces of
up to this identification.
The boundary maps in the cellular complex are as follows. If is a
-cell and
its attaching map (where
here denotes the
-skeleton of
), then the differential is
where runs over an enumeration of all
-cells
,
denotes the degree, and
is the map
induced by collapsing all of
except the cell
to a point.
In this particular case all of the boundary maps in the cellular complex are trivial, so the homology is free abelian on cells. To see this, note that if
is not surjective, then it necessarily has degree
since it is null-homotopic, so we reduce to the surjective case. In this case the
-cell
must be a face of the
-cell
, and since we’ve collapsed everything else we can reduce to the case that
, so that
is the top-dimensional cell. At this point we will cheat a little: if
in this case, then we would have
, but
is a compact orientable manifold and therefore must satisfy
.
In particular, the cell decomposition we gave above is minimal: it is not possible to give a cell decomposition with fewer cells. In addition, by Poincaré duality the cohomology can also be thought of as free abelian on cells, and moreover we can describe the cup product in terms of transverse intersections of submanifolds representing homology classes. We can do this by explicitly intersecting the cells above, but the following description is perhaps more elegant: if we think of
as
, then a subspace
represents a homology class if it is translation-invariant (given by the pushforward of a fundamental class). The images of two such subspaces
intersect transversely if
, and then their intersection
represents a homology class which Poincaré dualizes to the cup product of the Poincaré duals of
. In particular, note that the short exact sequence
implies that . Its Poincaré dual is therefore a class in
, which has the correct degree.
Method ???: the Lefschetz fixed point theorem
This method is not numbered because the argument is incomplete. Consider the map
where each is a positive integer equal to at least
. This map has
fixed points, since in each coordinate the fixed points of
are precisely the
th roots of unity. Each fixed point has index
. By the Lefschetz fixed point theorem it follows that
.
Knowing what we already know about the cohomology, it is tempting to identify a monomial on the LHS with a cohomology class on the RHS on which acts by multiplication by that monomial. We can do this as follows. For any subset
of indices we have a projection map
. Since
is a compact orientable manifold, it has a fundamental class generating its top cohomology. The map
induces a map on
such that any point has
preimages, hence
has degree
as a map on
, so acts on the fundamental class by multiplication by
. This action induces an action on the pullback of the fundamental class of
to
which is also by multiplication by
.
As the vary this argument shows that the cohomology classes arising in this way are all linearly independent, hence all contribute to the RHS of the Lefschetz fixed point theorem. The sum of the corresponding contributions
to the RHS exhaust all terms on the LHS, so if there is any more cohomology to be found then it isn’t being detected by
.
Method ???: Morse theory
There is a convenient choice of Morse function on given by
.
The gradient of this function is , and in particular it vanishes iff
for all
. There are therefore
critical points
, organized in batches of
critical points such that
coordinates are equal to
and
coordinates are equal to
. At such a point
of the second derivatives of each term
are equal to
and
are equal to
, with no other contributions to the second-order Taylor series expansion of
, so all critical points are nondegenerate (hence we do in fact have a Morse function) with index
. Morse theory then guarantees that
has the homotopy type of a CW-complex with
cells of dimension
.
This argument should be placed in the context of a Morse-theoretic proof of the Künneth formula; more generally, if are manifolds with Morse functions
, then
is a Morse function on the product
, and critical points of
are precisely products of critical points on the
, and so forth.
With more effort Morse theory even provides a complex computing the homology, but I wasn’t able to easily compute the differentials in it (they should all vanish in this case).
Interpretation
Our computations admit the following interpretation. Recall that is the Eilenberg-MacLane space
representing integral cohomology in the sense that there is a natural isomorphism
, where
denotes the space of homotopy classes of maps (or weak homotopy classes if
are not CW-complexes)
. It follows that
represents
-tuples of cohomology classes in
. By the Yoneda lemma, cohomology classes in
, or equivalently homotopy classes of maps
, can naturally be identified with natural transformations
.
Such natural transformations between cohomology functors are called cohomology operations, and the computations we did above imply that the only cohomology operations of this form are generated by wedge products under addition. (“Interesting” cohomology operations over , not generated by addition and the wedge product, require higher cohomology classes as input. The smallest one is a cohomology operation
; see this math.SE question.)
You could also compute this using group cohomology theory – in fact, it is essentially a trivial example of the Hochschild-Serre spectral sequence.
Yes, I’ve since learned several other methods to do this computation!
“With more effort Morse theory even provides a complex computing the homology, but I wasn’t able to easily compute the differentials in it (they should all vanish in this case).” more on this.
Would you please give me a reference for method 3?
I don’t know a reference.
The unit of the smash product is the two point space, S^0
Whoops; thanks.
This may be killing an ant with a flamethrower, but proceed by induction by applying the Leray-Serre spectral sequence to the fibre bundle $S^{1}\hookrightarrow T^{n} \to T^{n-1}$. Always collapses at $E_{2}^{p,q}$ for degree reasons. Morally, this is the same as the Kunneth formula solution.
(Real) Hodge theory: Take the obvious metric on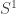 . The laplacian operator takes
. The laplacian operator takes 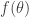 to
to 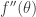 and takes
and takes  to
to  . The only periodic solution to
. The only periodic solution to 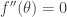 is taking
is taking  constant, so the only harmonic functions are the constant functions and the only harmonic 1-forms are multiples of
constant, so the only harmonic functions are the constant functions and the only harmonic 1-forms are multiples of 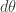 .
.
Switching from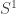 to
to  :
:
On any affine (or Stein) space, Cartan’s Theorem B implies that using holomorphic differential on $\mathbb{C}^{\ast}$, with
on $\mathbb{C}^{\ast}$, with  holomorphic, has a holomorphic anti-derivative if and only if it has residue zero at 0, so
holomorphic, has a holomorphic anti-derivative if and only if it has residue zero at 0, so 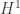 is
is  again.
again.
forms in the de Rham complex computes topological cohomology. A differential form
By a theorem of Grothendieck, we can replace holomorphic functions with polynomial functions in this setting. Sure enough, a Laurent polynomial has a Laurent polynomial anti-derivative if and only if the coefficient of
has a Laurent polynomial anti-derivative if and only if the coefficient of  is 0.
is 0.
Write as
as 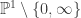 . I’ll abbreviate
. I’ll abbreviate  to
to  and
and  to
to  . Then Deligne computes the Hodge filtration on
. Then Deligne computes the Hodge filtration on  using a spectral sequence which collapses at
using a spectral sequence which collapses at  and gives us
and gives us  .
.
One could probably write down several more good computations by treating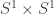 as an elliptic curve, but I’m out of time for now.
as an elliptic curve, but I’m out of time for now.
Reblogged this on citedcorpse and commented:
I like this concept a lot.
How about Lie algebra cohomology? The n-torus is a compact Lie group, so the corresponding Lie algebra cohomology computes its cohomology.
That’s what I’m using to compute the de Rham cohomology. But it didn’t seem worth being explicit about it in this example because of all the differentials are trivial.
The thing that’s messed up/wonderful about this is that it’s defined for Lie algebras of noncompact groups (like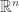 ), but when they’re also Lie algebras of compact groups, it’ll find the cohomology of the compact group. How does it know!!
), but when they’re also Lie algebras of compact groups, it’ll find the cohomology of the compact group. How does it know!!