Small factors in random polynomials over a finite field

November 10, 2012 by Qiaochu Yuan

Previously I mentioned very briefly Granville’s The Anatomy of Integers and Permutations, which explores an analogy between prime factorizations of integers and cycle decompositions of permutations. Today’s post is a record of the observation that this analogy factors through an analogy to prime factorizations of polynomials over finite fields in the following sense.

Theorem: Let $q$ be a prime power, let $n$ be a positive integer, and consider the distribution of irreducible factors of degree $1, 2, ... k$ in a random monic polynomial of degree $n$ over $\mathbb{F}_q$ . Then, as $q \to \infty$ , this distribution is asymptotically the distribution of cycles of length $1, 2, ... k$ in a random permutation of $n$ elements.

One can even name what this random permutation ought to be: namely, it is the Frobenius map $x \mapsto x^q$ acting on the roots of a random polynomial $f$ , whose cycles of length $k$ are precisely the factors of degree $k$ of $f$ .

Combined with our previous result, we conclude that as $q, n \to \infty$ (with $q$ tending to infinity sufficiently quickly relative to $n$ ), the distribution of irreducible factors of degree $1, 2, ... k$ is asymptotically independent Poisson with parameters $1, \frac{1}{2}, ... \frac{1}{k}$ .

Proof modulo some analytic details

By the cyclotomic identity, we have

$\displaystyle \sum_f t^{\deg f} = \frac{1}{1 - qt} = \prod_P \left( \frac{1}{1 - t^{\deg P}} \right) = \prod_{d \ge 1} \left( \frac{1}{1 - t^d} \right)^{M(q, d)}$

where the sum runs over all monic polynomials over $\mathbb{F}_q$ , the product runs over over all monic irreducible polynomials over $\mathbb{F}_q$ , and

$\displaystyle M(q, d) = \frac{1}{d} \sum_{r | d} \mu(r) q^{d/r}$

is the number of monic irreducible polynomials of degree $d$ over $\mathbb{F}_q$ . This is Euler product for the zeta function for $\mathbb{F}_q[x]$ . To get the results we want we need an analogue for polynomials over finite fields of the exponential formula which keeps track of how many factors of a given degree a polynomial has. Letting $c_i(f)$ denote the number of irreducible factors of degree $i$ of $f$ , this is given by

$\displaystyle \sum_f t^{\deg f} z_1^{c_1(f)} z_2^{c_2(f)} ... = \prod_P \left( \frac{1}{1 - z_{\deg P} t^{\deg P}} \right) = \prod_{d \ge 1} \left( \frac{1}{1 - z_d t^d} \right)^{M(q, d)}$ .

To get a generating function describing the joint moment generating function of the variables $c_1, c_2, ...$ we will also need to divide the terms corresponding to polynomials of degree $n$ by the number of such polynomials, which is $q^n$ . This is equivalent to replacing $t$ with $\frac{t}{q}$ , which gives

$\displaystyle \sum_f \frac{t^{\deg f}}{q^{\deg f}} z_1^{c_1(f)} z_2^{c_2(f)} ... = \prod_{d \ge 1} \left( \frac{1}{1 - \frac{z_d t^d}{q^d} } \right) ^{ M(q, d) }$ .

We are now in a position to take the limit $q \to \infty$ . We will do so somewhat cavalierly: since $M(q, d) \sim \frac{q^d}{d}$ as $q \to \infty$ and $d$ is fixed, we expect that

$\displaystyle \left( \frac{1}{1 - \frac{z_d t^d}{q^d}} \right)^{M(q, d)} \to \exp \left( \frac{z_d t^d}{d} \right)$

as $q \to \infty$ , hence the above generating in some sense approaches

$\displaystyle \exp \left( z_1 t + z_2 \frac{t^2}{2} + z_3 \frac{t^3}{3} + ... \right)$

as $q \to \infty$ , at least in the sense that their lower-order terms should match up reasonably well (where “lower-order” depends on $q$ ). But this is precisely

$\displaystyle \sum_{n \ge 0} \frac{t^n}{n!} \sum_{\sigma \in S_n} z_1^{c_1(\sigma)} z_2^{c_2(\sigma)} ...$

by the exponential formula.

Some comments on Granville’s analogy

The tripartite analogy between cycle decomposition of permutations, prime factorization of polynomials over a finite field, and prime factorization of integers can be made more specific as follows. There is a lot to say on this subject, but we will content ourselves with two sets of analogies.

First, the following three statements are analogous.

A random permutation of $d$ elements is a $d$ -cycle with probability $\frac{1}{d}$ .
A random monic polynomial of degree $d$ over $\mathbb{F}_q$ is irreducible with probability asymptotically $\frac{1}{d}$ (as $q \to \infty$ ).
An integer of size approximately $n$ is prime with probability approximately $\frac{1}{\log n}$ (the prime number theorem).

This suggests that the correct analogue of the degree of a positive integer $n$ is $\log n$ , an idea which is also suggested by the fact that the norm of a polynomial $f$ of degree $d$ over $\mathbb{F}_q$ is $q^d$ , since this is the size of $\mathbb{F}_q[x]/f(x)$ , whereas the norm of a positive integer $n$ is $n$ .

Second, the following three statements are analogous.

The distribution of cycles of length $1, 2, ... k$ of a random permutation of $n$ elements is asymptotically (as $n \to \infty$ ) independent Poisson with parameters $1, \frac{1}{2}, ... \frac{1}{k}$ .
The distribution of irreducible factors of degree $1, 2, ... k$ of a random monic polynomial over $\mathbb{F}_q$ of degree $n$ is asymptotically (as $q, n \to \infty$ with $q$ growing sufficiently fast relative to $n$ ) independent Poisson with parameters $1, \frac{1}{2}, ... \frac{1}{k}$ .
The distribution of prime factors in the intervals $[1, e], [e, e^2], ... [e^{k-1}, e^k]$ of a random integer in the interval $[e^{n-1}, e^n]$ is asymptotically (as $n \to \infty$ ) independent Poisson with parameters asymptotic to the sequence $1, \frac{1}{2}, ... \frac{1}{k}$ .

The third statement in this analogy is false as stated; for example, the distribution of prime factors in the interval $[1, e]$ is asymptotically geometric, not Poisson. It may be true if one takes $k \to \infty$ in addition to $n$ in a suitable way while throwing out small primes in a way dependent on $k$ and while changing “independent Poisson” to “independent asymptotically Poisson,” where this second use of “asymptotically” depends on $k$ .

I offer as weak evidence the following heuristic calculation. First, the probability that a large positive integer $n$ is divisible by some $m$ is $\frac{1}{m}$ . If $X$ is a random variable which takes on non-negative integer values, then a straightforward telescoping argument shows that

$\displaystyle \mathbb{E}(X) = \sum_{d \ge 1} \mathbb{P}(X \ge d)$ .

If $X$ is the exponent of a prime $p$ in the prime factorization of $n$ , then heuristically $\mathbb{P}(X \ge d) = \frac{1}{p^d}$ , so

$\displaystyle \mathbb{E}(X) = \sum_{d \ge 1} \frac{1}{p^d} = \frac{1}{p-1}$ .

There is a well-known asymptotic for the sum of the reciprocals of the primes which implies that

$\displaystyle \sum_{p \le n} \frac{1}{p-1} = \log \log n + O(1)$

and consequently the expected number of prime factors (counted with multiplicity) in the interval $[e^{k-1}, e^k]$ of a large positive integer is heuristically asymptotically $\log k - \log (k-1) \sim \frac{1}{k}$ .

(Edit, 11/11/12:) The heuristic calculation can be taken further as follows. Letting $c_p$ denote the random variable describing the exponent of $p$ in a random prime factorization, we have heuristically $\mathbb{P}(c_p = k) = \left( 1 - \frac{1}{p} \right) \frac{1}{p^k}$ and therefore heuristically the moment generating function

$\displaystyle \mathbb{E}(e^{tc_p}) = \left( 1 - \frac{1}{p} \right) \sum_{k \ge 0} \frac{e^{tk}}{p^k} = \frac{1 - \frac{1}{p}}{1 - \frac{e^t}{p}}$ .

For prime factorizations of large positive integers we expect the variables $c_p, p \in [e^{k-1}, e^k]$ to heuristically be asymptotically independent, so heuristically their sum has moment generating function

$\displaystyle \prod_{p \in [e^{k-1}, e^k]} \frac{1 - \frac{1}{p}}{1 - \frac{e^t}{p}}$ .

By the PNT, there are approximately $\frac{e^k - e^{k-1}}{k}$ primes in this interval. Let us blithely pretend that they all have absolute value approximately $e^k - e^{k-1}$ , because this is somewhere between $e^{k-1}$ and $e^k$ and gives the expected value we computed above. Then we are reduced to a calculation very similar to the calculation over finite fields. Namely, we get a moment generating function

$\displaystyle \left( 1 - \frac{1}{e^k - e^{k-1}} \right)^{ \frac{e^k - e^{k-1}}{k} } \left( 1 - \frac{e^t}{e^k - e^{k-1}} \right)^{ - \frac{e^k - e^{k-1}}{k} }$

and as $k \to \infty$ this is asymptotic to

$\displaystyle \exp \left( \frac{1}{k} (e^t - 1) \right)$

which is the moment generating function of a Poisson random variable with parameter $\frac{1}{k}$ as expected.

Posted in math.CO, math.NT, math.PR | Tagged generating functions, MaBloWriMo | 4 Comments

4 Responses

on November 11, 2012 at 5:08 pm | Reply JSE

Briefly: a question like “how many quadratic factors does the average squarefree degree-n polynomial have?” can be expressed in terms of the cohomology of a certain local system on the configuration space of n points in the affine line. These local systems are all representations of the fundamental group of configuration space (i.e. the braid group on n strands) which factor through the map from the braid group to S_n, whose kernel is the pure braid group (which here is manifested as the fundamental group of the space of ORDERED configurations, which covers the usual configuration space with Galois groups S_n.) This means that the statistics you want can be computed from the cohomology of the ordered configuration space (= cohomology of pure braid group) but you need to know what that cohomology is not just as a vector space but as a representation of S_n. (You need to know how Frobenius acts too but in this case it’s not hard to show that everything in sight is Tate type.) Anyway, this last thing is exactly the kind of situation contemplated in the FI-module papers.

But let me emphasize that this is an unnecessarily difficult way to obtain statements like the ones you prove in the post! I’m more saying “this is where these statements fit in to a stable cohomology story” than “this is how you should prove those statements.”
- on November 11, 2012 at 5:16 pm | Reply Qiaochu Yuan
  
  Interesting. Can you tell a similar story for polynomials that aren’t squarefree?
on November 11, 2012 at 8:55 am | Reply JSE

One relevant reference for this stuff:

Click to access tavare.pdf

In fact it gets even more fun when you hold q fixed and just let n go to infinity — see e.g.

Click to access ABT93.pdf

I blogged a while ago about how you can think of the problem of computing the probability that a random polynomial over F_q is squarefree as a question about the cohomology of the braid group (not, of course, the easiest way to solve that problem!) In the same way, these questions about short cycles of random polynomials over F_q have to do with the cohomology of the _pure_ braid group, and the fact that the short cycles approach a limiting joint distribution (even with fixed q) has to do with the fact that that cohomology is “finitely generated as an FI-module” in the sense of the stuff that Tom Church, Benson Farb and I are working on. Happy to talk about this more! (but probably not in the somewhat constrained venue of blog comment box…)
- on November 11, 2012 at 1:39 pm | Reply Qiaochu Yuan
  
  Thanks for the references! I’ve read those blog posts and had some vague suspicion that they might be relevant. Can you elaborate on the relationship to the pure braid group? The variety this comment suggests is relevant seems to be, say, the complement of the locus where the discriminant vanishes in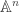 $\mathbb{A}^n$ , but I’m not sure what this has to do with random polynomials that aren’t necessarily squarefree.

Comments RSS

	ZW on The double commutant theo…
	auto on More about the Schrödinger equ…
	Jaromir Kuben on Meditation on the Sylow theore…
	Qiaochu Yuan on Meditation on the Sylow theore…
	Qiaochu Yuan on Some remarks on the infinitude…

Annoying Precision

"A good stock of examples, as large as possible, is indispensable for a thorough understanding of any concept, and when I want to learn something new, I make it my first job to build one." – Paul Halmos