Suitably nice groupoids have a numerical invariant attached to them called groupoid cardinality. Groupoid cardinality is closely related to Euler characteristic and can be thought of as providing a notion of integration on groupoids.
There are various situations in mathematics where computing the size of a set is difficult but where that set has a natural groupoid structure and computing its groupoid cardinality turns out to be easier and give a nicer answer. In such situations the groupoid cardinality is also known as “mass,” e.g. in the Smith-Minkowski-Siegel mass formula for lattices. There are related situations in mathematics where one needs to describe a reasonable probability distribution on some class of objects and groupoid cardinality turns out to give the correct such distribution, e.g. the Cohen-Lenstra heuristics for class groups. We will not discuss these situations, but they should be strong evidence that groupoid cardinality is a natural invariant to consider.
Axiomatics
For convenience, in this section we will restrict to essentially finite groupoids, namely those groupoids equivalent to groupoids with finitely many objects and morphisms.
Associated to any essentially finite groupoid is a rational number, its groupoid cardinality
, which is uniquely determined by the following four properties, analogous to the properties uniquely specifying Euler characteristic:
- Cardinality:
, where
is the groupoid with one object and one morphism.
- Homotopy invariance: If
(
is equivalent to
), then
.
- Gluing:
.
- Covering: If
is an
-sheeted covering map, then
.
A covering map of groupoids is a functor which is surjective on objects and which satisfies the unique path lifting property: if
is a morphism in
and
is an object in
such that
, then there exists a unique morphism
in
such that
. This axiomatizes the path lifting property satisfied by a covering map of topological spaces. A covering map is
-sheeted if the preimage of every object in
consists of
objects in
.
The homotopy invariance and gluing axioms imply that groupoid cardinality is completely determined by how it behaves on one-object groupoids , where
is a finite group (since we are assuming essential finiteness). Associated to any such groupoid is a canonical
-sheeted cover
where is the action groupoid for the action of
on itself (the objects are the elements of
and there is a unique morphism
between any pair of objects). This covering map sends the morphism
to the element
of
. The notation
is by strong analogy with the theory of classifying spaces.
Since is equivalent to a point,
by the cardinality axiom, and the covering axiom then implies that
. In conclusion, we find that if
is an essentially finite groupoid then, writing the skeleton of
as
we have
.
In words, the groupoid cardinality of is a weighted sum over the isomorphism classes of objects in
, where an object is weighted by the size of its automorphism group. Intuitively speaking, we can think of the objects of
as being “cut up” by their automorphism groups into fractional points.
Groupoid cardinality has other properties besides the above that make it a natural measure of the size of a groupoid.
Proposition: Let be essentially finite groupoids. Then their product
is also essentially finite, and
.
Proof. A groupoid is essentially finite if and only if it has finitely many isomorphism classes and the objects in each isomorphism class have finitely many automorphisms. This condition is preserved under finite products; moreover, if
and
then
which gives the desired result.
Alternatively, one could show that satisfied all of the axioms above.
Proposition: Let be a finite set and
be a finite group acting on
. Then the groupoid cardinality of the action groupoid or weak quotient
is
.
Note that this is badly false for the set-theoretic quotient , a point which trips up many beginners in combinatorics.
The idea of the proof is that we would like to apply the covering axiom to the natural map (thinking of
as a discrete groupoid), except that this map isn’t a covering map unless the action of
is free. However, it can be replaced by a covering map up to equivalence (a kind of fibrant replacement) essentially using the Borel construction.
Proof. Instead of considering , consider the equivalent groupoid
, which consists of pairs
where
, and where there is a unique morphism
for every
. Since
acts on both
and
, it acts on this product, and so we can consider the action groupoid
and the corresponding map
.
Since acts freely on
, this map is a
-sheeted covering map. Moreover,
and
. We can now apply the covering axiom, and the conclusion follows.
For a more pedestrian proof, observe that it suffices by the gluing axiom to prove the statement in the case that the action of on
is transitive, where it reduces to the orbit-stabilizer theorem.
Digression: random finite sets
The definition of groupoid cardinality can be extended to tame groupoids, namely those groupoids such that the sum
converges. For any such groupoid, there is a natural probability measure on given by the condition that a given isomorphism class
occurs with probability
.
For example, if is the groupoid of finite sets and bijections, then
and the finite set of cardinality occurs with probability
. In other words, “size of a random finite set” is Poisson with parameter
. It is unclear to me what the significance of this observation is, if any.
More generally, let be a finite set and consider the groupoid of
-colored finite sets. This is the groupoid whose objects are finite sets
equipped with a map
(assigning to each element of
its color) and whose morphisms are bijections
compatible with colors. The cardinality of this groupoid may be computed in two ways. On the one hand, there are
isomorphism types of objects where
, and the groupoid consisting these isomorphism types is equivalent to the action groupoid of
acting on the set of all functions from an
-element set to
, hence the groupoid cardinality is
.
On the other hand, the groupoid of -colored finite sets is equivalent to the product of
copies of the groupoid of finite sets; the equivalence is given by sending an
-colored finite set to the finite sets given by the elements of each color. It is not hard to show that for tame groupoids we have
, hence the groupoid cardinality is
.
Hence “size of a random -colored finite set” is Poisson with parameter
, and along the way to seeing this we have shown that two ways of defining
give the same answer (and also implicitly given a combinatorial proof that
).
There is much more to say about these kinds of arguments, much of which has been said by John Baez at some point, but I don’t know a place where all of the relevant links have been collected. One place to start and work backwards from is week300.
Groupoid cardinality and Euler characteristic
The axiomatic definition of groupoid cardinality suggests that it ought to behave like Euler characteristic, except that the Euler characteristic of familiar spaces are integers and groupoid cardinality is not an integer. However, there is a nice sense in which the Euler characteristic of ought to be
.
is a groupoid model of a classifying space of
, also denoted
, which for discrete groups has two equivalent definitions. It is the unique (up to homotopy) connected space such that
and such that all higher homotopy groups are trivial; in other words, it is the Eilenberg-MacLane space
. Such spaces are also known as aspherical spaces.
The classifying space is also the space which represents, in a suitable homotopy category, the functor sending a topological space to its set of principal
-bundles. When
is a discrete group, this is the same thing as a
-cover, but the definition in terms of bundles also generalizes to topological groups.
Example. is the circle
.
Example. More generally, a nice connected space is a
for
if and only if its universal cover is contractible; in particular any hyperbolic manifold has this property.
Example. is infinite real projective space
.
The sense in which ought to be
for
finite is the following. Recall that if
is, say, a finite CW complex, we should have
where is the number of
-cells of
. There is a distinguished model of
(the space) having a cell decomposition in which
, and thus we ought to have
by summing a divergent geometric series! I learned this from MO. This can be seen more explicitly for , for example, which has a single cell in each dimension and therefore whose Euler characteristic ought to be Grandi’s series
.
[…] blogs très sympas sur le sujet ici et […]
[…] It is important to count only one object from each isomorphism class since we want the notion of groupoid cardinality to be invariant under equivalences of groupoids (in the sense of category theory) and every category is equivalent to it’s skeleton. For further motivation for the idea of a groupoid cardinality, see Qiaochu Yuan’s post on them […]
[…] number of axioms such as these (similar to the axioms that determine Euler characteristic); see this blog post of Qiaochu Yuan for […]
[…] Euler characteristic, which in some sense generalizes both the usual Euler characteristic and groupoid cardinality. We will only compute this number for (classifying spaces of) finitely generated groups which are […]
[…] prove and apply a version of the exponential formula that comes from relating (weighted) groupoid cardinalities of a groupoid and of the free symmetric monoidal groupoid on […]
[…] (thinking of taking coinvariants with respect to an -action as categorifying dividing by , in accordance with the general yoga of groupoid cardinality.) […]
Re the significance of the fact that the cardinality of a random finite set is Poisson with mean 1; there are lots of situations where some finite set of covers is NOT naturally a group, as in Cohen-Lenstra, but merely a finite set, and in cases like this you might naturally expect to find a Poisson distribution. E.G. in the paper of Dunfield and Thurston you find that set of Q-covers of a “random 3-manifold” in their model is a random finite set, when Q is a finite simple group. In the “Cohen-Lenstra” spirit one might guess along similar lines that if N is a random positive squarefree integer, the number of totally real quintic fields with discriminant N is distributed as Poisson with mean 1/120.
Re nice properties of groupoid uniform distribution — in my paper with Cais and Zureick-Brown we used this to make an argument that was really horrible nice and clean instead…
Also, see http://quomodocumque.wordpress.com/2008/11/26/tom-leinster-on-entropy-diversity-and-cardinality/
for a discussion of an application (by Leinster) to mathematical biology!
Thanks.
So is there a good reference for what the “right” Euler characteristic of a space should be? One that gives consistent results in all situations. Or a reasoned classification of possible Euler characteristics?
I don’t know. Even for, say, nice noncompact smooth manifolds there are at least two reasonable notions of Euler characteristic, namely the ordinary one coming from singular or de Rham cohomology and compactly supported Euler characteristic, coming from compactly supported de Rham cohomology. The latter is not invariant up to homotopy (but is invariant up to proper homotopy?) but satisfies the correct gluing laws (e.g. I think has compactly supported Euler characteristic
has compactly supported Euler characteristic 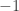 instead of
instead of  and this is compatible with the decomposition of
and this is compatible with the decomposition of 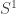 into
into  and a point).
and a point).
Thanks for the example.
A few remarks, not very interesting:
For algebraic varieties I found this paper
Click to access Euler.pdf
about Euler characteristics, which mentions another reasonable characteristic, defined from intersection homology. Then I remembered that (Euler) characteristics are more generally any homomorphism between K-groups or K-rings, or at least with one K-group as target or domain, and usually with a more complicated domain, perhaps geometric (manifolds, varieties, etc.), and a simpler more linear target -the usual Euler characteristic is to K(N). This includes (Lang’s?) definition of Euler-Poincaré mapping with K_0 of the category of modules as domain. So I guess Euler characteristics should probably be seen as available in a variety of flavors: depending on what we study, what we want them to retain or forget (in the case of the interval, that it is contractible, or that it has 1 point compactification the circle).