Moments, Hankel determinants, orthogonal polynomials, Motzkin paths, and continued fractions

« A meditation on semiadditive categories

Noncommutative probability and group theory »

Moments, Hankel determinants, orthogonal polynomials, Motzkin paths, and continued fractions

September 18, 2012 by Qiaochu Yuan

Previously we described all finite-dimensional random algebras with faithful states. In this post we will describe states on the infinite-dimensional $^{\dagger}$ -algebra $\mathbb{C}[x]$ . Along the way we will run into and connect some beautiful and classical mathematical objects.

A special case of part of the following discussion can be found in an old post on the Catalan numbers.

Positivity and Hankel determinants

Consider the $^{\dagger}$ -algebra $\mathbb{C}[x]$ with involution given by extending $x^{\dagger} = x$ ; in other words, the free complex $^{\dagger}$ -algebra on a self-adjoint element. A state $\mathbb{E} : \mathbb{C}[x] \to \mathbb{C}$ is uniquely determined by the moments $m_n = \mathbb{E}(x^n)$ which are real since the $x^n$ are all self-adjoint and which satisfy $m_0 = 1$ . Positivity is equivalent to the condition that for any $c(x) = c_0 + c_1 x + ... + c_n x^n \in \mathbb{C}[x]$ we have

$\displaystyle \mathbb{E}(c(x)^{\dagger} c(x)) = \sum_{i, j} \overline{c_i} c_j m_{i+j} \ge 0$

and this condition characterizes states on $\mathbb{C}[x]$ . That this condition actually characterizes Borel measures on the real line $\mathbb{R}$ is the content of the solution to the Hamburger moment problem, although we will not use this fact. In discussing examples, we will make implicit use of the fact that various kinds of Borel measures on $\mathbb{R}$ are uniquely determined by their moments thanks to results like Carleman’s condition, but only in order to identify these measures from their moments.

Note that by the universal property, if $A$ is any random algebra and $a \in A$ any self-adjoint element, then there is a unique morphism $\mathbb{C}[x] \to A$ of $^{\dagger}$ -algebras sending $x$ to $a$ , and pulling back the state on $A$ gives a state on $\mathbb{C}[x]$ . Consequently, everything we are about to say about states on $\mathbb{C}[x]$ places restrictions on states on any random algebra (more precisely, on moment sequences of self-adjoint elements of any random algebra).

The states which are not faithful are straightforward to describe.

Proposition: Let $\mathbb{E}$ be a state on $\mathbb{C}[x]$ which is not faithful. If $c$ is a nonzero self-adjoint element of minimal degree such that $\mathbb{E}(c^2) = 0$ , then $\mathbb{E}$ is a finite sum of Dirac measures supported at the roots of $c$ , all of which are real.

Proof. Note that “self-adjoint” here is equivalent to having real coefficients. We first show that the roots of $c$ are all real. Suppose by contradiction that $c = c(x)$ has a complex root $r + si$ with $s \neq 0$ . Then it is divisible by $(x - r - si)(x - r + si)$ . Writing $c(x) = d(x) ((x - r)^2 + s^2)$ where $d$ is self-adjoint, we have

$0 = \mathbb{E}(c^2) \ge \mathbb{E}(d^2 s^4)$ .

By positivity of $\mathbb{E}$ , it follows that $\mathbb{E}(d^2 s^4) = 0$ , and since $s^4 > 0$ , it follows that $\mathbb{E}(d^2) = 0$ , which contradicts the assumption that $c$ has minimal degree. Hence all of the roots of $c$ are real.

By the division algorithm, we can write any $a \in \mathbb{C}[x]$ in the form $a = cq + r$ where $\deg r < \deg c$ . By Cauchy-Schwarz we have $\mathbb{E}(cq) = 0$ , hence

$\mathbb{E}(a) = \mathbb{E}(cq + r) = \mathbb{E}(r)$ .

Let $x_1, ... x_n$ be the real roots of $c$ . Since $\deg r < \deg c$ , by Lagrange interpolation we know that $r$ can be written

$\displaystyle r(x) = \sum_{k=1}^n r(x_i) \ell_i(x)$

where

$\displaystyle \ell_i(x) = \prod_{1 \le m \le n, m \neq i} \frac{x - x_m}{x_i - x_m}$

are the Lagrange interpolation polynomials, which do not depend on $r$ . Consequently,

$\displaystyle \mathbb{E}(a) = \mathbb{E}(r) = \sum_{k=1}^n r(x_i) \mathbb{E}(\ell_i) = \sum_{k=1}^n a(x_i) \mathbb{E}(\ell_i)$

which is a finite sum of Dirac measures supported at the points $x_i$ as desired. $\Box$

The corresponding universal statement is the following: if $a$ is a self-adjoint element of any random algebra $A$ which has a minimal polynomial, then the state on $A$ restricted to $\mathbb{C}[a]$ is a finite sum of Dirac measures supported on the spectrum of $a$ (which is finite).

As for the faithful states, we can say the following. Faithfulness is equivalent to the condition that for every $n$ the Hankel matrix

$\displaystyle H_n = \left[ \begin{array}{cccc} m_0 & m_1 & \hdots & m_{n-1} \\ m_1 & m_2 & \hdots & m_n \\ \vdots & \vdots & \ddots & \vdots \\ m_{n-1} & m_n & \hdots & m_{2n-2} \end{array} \right]$

with entries $(H_n)_{i, j} = m_{i+j}$ is positive-definite. This is because $H_n$ is the symmetric matrix describing the restriction of the inner product $\langle a, b \rangle = \mathbb{E}(a^{\dagger} b)$ to the subspace $V_n$ of polynomials of degree less than $n$ . In particular, if $\mathbb{E}$ is faithful, the Hankel determinants $h_n = \det H_n$ are positive. For example, $h_2 = m_2 - m_1^2$ is the variance $\text{Var}(x) = \mathbb{E}(x^2) - \mathbb{E}(x)^2$ .

Proposition (Sylvester’s criterion): $H_n$ is positive-definite if and only if $h_k > 0$ for all $k \le n$ .

Corollary: A moment sequence $m_n$ determines a faithful state if and only if $h_n > 0$ for all $n$ .

Proof. We observed one direction above. In the other direction, we prove the contrapositive. Note that $H_1$ is always positive-definite. We proceed by induction. Assume that $H_{n-1}$ is positive-definite. By the spectral theorem, $H_n$ has an orthonormal basis of eigenvectors, which we may take to be self-adjoint elements of $V_n$ . Since $h_n > 0$ , it follows that $H_n$ has an even number of eigenvectors with negative eigenvalues. Suppose by contradiction that it has at least one, hence at least two, such eigenvectors $v_i, v_j$ with negative eigenvalues $\lambda_i, \lambda_j$ . Then

$\displaystyle (a v_i + b v_j)^T H_n (a v_i + b v_j) = \lambda_i a^2 + \lambda_j b^2 \le 0$

with strict inequality if either $a$ or $b$ is nonzero. On the other hand, there exists some choice of $a, b$ such that $a v_i + b v_j \in V_{n-1}$ , from which it follows that $H_{n-1}$ is not positive-definite; contradiction.

Hence $H_n$ has only positive eigenvalues, so is positive-definite. $\Box$

So we have reduced the problem of determining whether a moment sequence describes a state on $\mathbb{C}[x]$ to the problem of determining whether its Hankel determinants are non-negative. Unfortunately, it is not at all obvious how to compute Hankel determinants. We give without proof several evaluations of Hankel determinants below; the proofs will be subsumed in a more general result later in the post.

Example. Consider the moment sequence $m_n = \frac{1}{n+1}$ . The corresponding Hankel matrices are the Hilbert matrices

$\displaystyle H_n = \left[ \begin{array}{cccc} 1 & \frac{1}{2} & \hdots & \frac{1}{n} \\ \frac{1}{2} & \frac{1}{3} & \hdots & \frac{1}{n+1} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{1}{n} & \frac{1}{n+1} & \hdots & \frac{1}{2n-1} \end{array} \right]$

and the corresponding Hankel determinants are

$\displaystyle \frac{1}{h_n} = n! \prod_{i=1}^{2n-1} {i \choose \lfloor i/2 \rfloor}$ .

The corresponding state on $\mathbb{C}[x]$ describes the uniform distribution on $[0, 1]$ .

Example. Consider the moment sequence $m_n = B_n$ , the Bell numbers. The corresponding Hankel determinants are

$\displaystyle h_n = \prod_{i=1}^{n-1} i!$ .

The corresponding state on $\mathbb{C}[x]$ describes the Poisson distribution with parameter $1$ .

Example. Consider the moment sequence with odd terms $m_{2n-1} = 0$ and even terms

$\displaystyle m_{2n} = 1 \cdot 3 \cdot ... \cdot (2n-1)$ .

The corresponding Hankel determinants are again

$\displaystyle h_n = \prod_{i=1}^{n-1} i!$ .

The corresponding state on $\mathbb{C}[x]$ describes the Gaussian distribution with mean $0$ and variance $1$ . As a corollary, the Hankel determinants of a moment sequence do not uniquely determine it.

Example. Consider the moment sequence $m_n = n!$ . The corresponding Hankel determinants are

$\displaystyle h_n = \prod_{i=1}^{n-1} i!^2$ .

The corresponding state on $\mathbb{C}[x]$ describes the exponential distribution with mean $1$ .

Example. Consider the moment sequence with odd terms $m_{2n-1} = 0$ and even terms $m_{2n} = C_n$ , the Catalan numbers. The corresponding Hankel determinants are

$\displaystyle h_n = 1$ .

The corresponding state on $\mathbb{C}[x]$ describes the Wigner semicircle distribution with radius $2$ . The semicircle distribution is important in free probability, where it takes on a role analogous to the Gaussian distribution in a noncommutative version of the central limit theorem. It also appears in number theory as the Sato-Tate distribution, where it comes from the distribution of traces of a random element of $\text{SU}(2)$ .

Example. Consider the moment sequence $m_n = C_n$ . The corresponding Hankel determinants are again

$\displaystyle h_n = 1$ .

The corresponding state on $\mathbb{C}[x]$ describes a random variable which is the square of a Wigner semicircularly distributed random variable.

Non-example. This example occurred a few years ago at the Secret Blogging Seminar. Consider the moment sequence with odd terms $m_{2n-1} = 0$ and even terms

$\displaystyle m_{2n} = \frac{3n+1}{n+1} {2n \choose n}$ .

The third Hankel determinant is

$\displaystyle h_3 = \det \left[ \begin{array}{ccc} 1 & 0 & 4 \\ 0 & 4 & 0 \\ 4 & 0 & 14 \end{array} \right] = -8$ .

Hence this moment sequence does not define a state (and consequently cannot describe a random variable).

Orthogonal polynomials and Motzkin paths

Faithful states on $\mathbb{C}[x]$ are closely related to the classical theory of orthogonal polynomials. The starting point is that $\mathbb{E}$ is a faithful state on $\mathbb{C}[x]$ if and only if $\langle a, b \rangle = \mathbb{E}(a^{\dagger} b)$ defines an inner product on $\mathbb{C}[x]$ . Applying the Gram-Schmidt process with a slightly different normalization to the basis $\{ 1, x, x^2, ... \}$ , we obtain a sequence $p_n$ of monic self-adjoint polynomials of degree $n$ , uniquely determined by the moment sequence $m_n = \mathbb{E}(x^n)$ , such that

$\displaystyle \langle p_n, p_m \rangle = \mathbb{E}(p_n p_m) = 0$

whenever $n \neq m$ . (In addition, $\mathbb{E}(p_n^2) > 0$ by faithfulness.) These are the orthogonal polynomials associated to $\mathbb{E}$ (equivalently, to the moment sequence $m_n$ ).

Example. For a state describing a Wigner semicircular distribution with radius $1$ , the corresponding polynomials are (up to normalization) the Chebyshev polynomials of the second kind.

Example. For a state describing a Gaussian distribution with mean $0$ and variance $1$ , the corresponding polynomials are the probabilist’s Hermite polynomials.

Example. For a state describing the uniform distribution on $[-1, 1]$ , the corresponding polynomials are (up to normalization) the Legendre polynomials.

Example. For a state describing the exponential distribution with mean $1$ , the corresponding polynomials are (up to normalization) the Laguerre polynomials.

The moments $m_n = \mathbb{E}(x^n)$ can be evaluated in terms of the orthogonal polynomials $p_n$ as follows. First, by construction $p_k$ is orthogonal to all polynomials of degree at most $k-1$ . Since $x$ is self-adjoint with respect to the inner product above, $xp_k$ is orthogonal to all polynomials of degree at most $k-2$ . It follows that the polynomials $xp_k, p_{k+1}, p_k, p_{k-1}$ are orthogonal to all polynomials of degree at most $k-2$ but have degree at most $k+1$ , hence lie in a $3$ -dimensional subspace of $\mathbb{C}[x]$ . Moreover, by orthogonality $p_{k+1}, p_k, p_{k-1}$ are linearly independent. Hence there exists a nontrivial linear dependence of the form

$\displaystyle xp_k = p_{k+1} + a_k p_k + b_k p_{k-1}$

where the coefficient of $p_{k+1}$ is determined by comparing leading coefficients. Thus the matrix of the linear operator given by multiplication by $x$ with respect to the basis $\{ p_0, p_1, p_2 ... \}$ is tridiagonal: it begins

$\displaystyle \left[ \begin{array}{ccccc} a_0 & b_1 & 0 & 0 & \hdots \\ 1 & a_1 & b_2 & 0 & \hdots \\ 0 & 1 & a_2 & b_3 & \hdots \\ 0 & 0 & 1 & a_3 & \hdots \\ \vdots & \vdots & \vdots & \vdots & \ddots \end{array} \right]$ .

Corollary: $p_n$ is the characteristic polynomial of the matrix

$\displaystyle J_n = \left[ \begin{array}{ccccc} a_0 & b_1 & 0 & \hdots & 0 \\ 1 & a_1 & b_2 & \hdots & 0 \\ 0 & 1 & a_2 & \hdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \hdots & a_{n-1}. \end{array} \right]$ .

Proof. Multiplication by $x$ has characteristic polynomial $p_n$ on $\mathbb{C}[x]/p_n(x)$ , which has basis $\{ p_0, ... p_{n-1} \}$ , and the above is the matrix by which $x$ acts in this basis. Alternately, this can be proven by induction on $n$ using the recurrence relation above. $\Box$

It will be convenient to think of the above matrix as the weighted adjacency matrix of a weighted graph $G$ with vertex set the non-negative integers $\mathbb{Z}_{\ge 0}$ and, for every $k \in \mathbb{Z}_{\ge 0}$ , three edges: an edge to $k+1$ with weight $1$ , an edge to $k$ with weight $a_k$ , and an edge to $k-1$ with weight $b_k$ .

The $n^{th}$ power of this matrix describes the sums of weights of paths of length $n$ in this graph, and these weights describe the action of multiplication by $x^n$ with respect to the basis $\{ p_0, p_1, p_2, ... \}$ . The corresponding paths (disregarding weights) are Motzkin paths, and they are counted by the Motzkin numbers $M_n$ .

In particular, $\mathbb{E}(x^n) = \mathbb{E}(x^n p_0)$ is equal to the sum of the weights of all closed walks in $G$ from $0$ to itself of length $n$ ; this sum contains $M_n$ terms, one for each Motzkin path, and may be thought of as a weighted Motzkin number. The first few such sums are as follows:

$\displaystyle \mathbb{E}(1) = 1$

$\displaystyle \mathbb{E}(x) = a_0$

$\displaystyle \mathbb{E}(x^2) = a_0 \mathbb{E}(x) + b_1$

$\displaystyle \mathbb{E}(x^3) = a_0 \mathbb{E}(x^2) + a_1 b_1 + b_1 a_0$

$\displaystyle \mathbb{E}(x^4) = a_0 \mathbb{E}(x^3) + b_1 a_0^2 + b_1^2 + a_1 b_1 a_0 + a_1^2 b_1 + b_2 b_1$ .

Example. For the Wigner semicircular distribution with $R = 2$ , we have $a_n = 0, b_n = 1$ for all $n$ . The above expression for moments then reduces to a sum over Motzkin paths which never stay at a given vertex, hence over Dyck paths, which are counted by the Catalan numbers. There are no paths of odd length, and a path of length $2n$ has weight $1$ . This gives $\mathbb{E}(x^{2n-1}) = 0$ and $\mathbb{E}(x^{2n}) = C_n$ as expected.

The combinatorial description of moments in terms of Motzkin paths leads to the following beautiful continued fraction expansion.

Theorem: We have an equality of formal power series

$\displaystyle \sum_{n \ge 0} m_n t^n = \frac{1}{1 - a_0 t - \frac{b_1 t^2}{1 - a_1 t - \frac{b_2 t^2}{1 - a_2 t - ...}}}$ .

Proof. This is more difficult to formalize than to understand. Consider the weighted graph $G$ described above. Let $G_{\ge n}$ be the graph obtained from $G$ by deleting the vertices $\{ 0, 1, ... n-1 \}$ (and all corresponding edges), and let $W_n$ be the set of all paths from $n$ to $n$ in $G_{\ge n}$ . The combinatorial content of the above theorem is that a path in $W_n$ has a unique decomposition into a sequence of paths of the following two forms:

A loop $n \to n$ (weight $a_n$ , length $1$ ), or
A step $n \to n+1$ (weight $1$ , length $1$ ), a path in $W_{n+1}$ , and a step $n+1 \to n$ (weight $b_{n+1}$ , length $1$ ).

Let $\omega(W_n)$ denote the sum of all weights of all paths in $W_n$ , weighted in addition by $t^{\text{length}}$ . Then $\omega(W_0) = \sum m_n t^n$ , and the above argument shows that

$\displaystyle \omega(W_n) = \frac{1}{1 - a_n t - b_{n+1} t^2 \omega(W_{n+1})}$ .

Applying this identity $k$ times verifies the desired equality $\bmod t^k$ , and taking $k \to \infty$ gives the result by the universal property of formal power series. $\Box$

A converse result

We saw above that we can associate to a faithful state $\mathbb{E}$ on $\mathbb{C}[x]$ a sequence $p_n$ of monic polynomials of degree $n$ such that $p_0 = 1$ and

$\displaystyle xp_n = p_{n+1} + a_n p_n + b_n p_{n-1}$

for some pair of sequences of real numbers $a_n, b_n$ uniquely determined by $\mathbb{E}$ . This pair of sequences in turn uniquely determines the sequence of polynomials $p_n$ , hence uniquely determines the state $\mathbb{E}$ via the conditions $\mathbb{E}(p_0) = 1$ and $\mathbb{E}(p_n) = 0, n \ge 1$ .

Given an arbitrary such pair of real sequences, it is natural to ask when the corresponding linear functional $\mathbb{E}$ determines a faithful state.

Proposition: If $n \neq m$ , then $\mathbb{E}(p_n p_m) = 0$ , and $\mathbb{E}(p_n^2) = b_1 b_2 ... b_n$ .

Proof. If $n \neq m$ , assume WLOG that $n < m$ . Write $p_n = \sum_{i=0}^n a_i x^i$ and apply the recurrence above to

$\displaystyle p_n p_m = \sum_{i=0}^n a_i x^i p_m$

to write it in the basis $\{ p_0, p_1, p_2, ... \}$ . Then $p_0$ does not appear as a term. One way to see this is to use the combinatorial interpretation; the coefficients in $x^i p_m$ count paths on the weighted graph $G$ starting at $m$ of length $i < n$ , and such a path cannot return to the origin. Hence by construction $\mathbb{E}(p_n p_m) = 0$ .

If $n = m$ , then applying the recurrence to $p_n p_n$ we see that the only contribution to the coefficient of $p_0$ comes from the unique path from $n$ to $0$ of length $n$ , which has weight $b_1 b_2 ... b_n$ as desired. $\Box$

Corollary (Favard’s theorem): The linear functional on $\mathbb{C}[x]$ associated to a pair of real sequences $a_n, b_n$ as above is a faithful state if and only if $b_n > 0$ for all $n$ .

Proof. Since the $p_n$ are orthogonal, $\mathbb{E}$ is faithful if and only if $\mathbb{E}(p_n^2) > 0$ for all $n$ . $\Box$

This gives us a method to construct faithful states on $\mathbb{C}[x]$ without computing Hankel determinants: we can instead write down a sequence $a_n$ of real numbers and another sequence $b_n$ of positive real numbers, then compute the corresponding orthogonal polynomials. The corresponding moment sequence can be computed using Motzkin paths or using the continued fraction. Alternatively, given a moment sequence which we suspect determines a faithful state, we can write down what we suspect the corresponding orthogonal polynomials are and compute the sequences $a_n$ and $b_n$ to verify that $b_n > 0$ for all $n$ .

Example. Taking $a_n = 0, b_n = 1$ for all $n$ gives the Wigner semicircular distribution with $R = 2$ .

Computing Hankel determinants

We now give the promised result which explains the Hankel determinants given without proof above.

Theorem: With notation as above, we have

$\displaystyle h_n = \prod_{i=1}^{n-1} b_1 b_2 ... b_i = \prod_{i=1}^{n-1} b_i^{n-i}$

Proof 1. First, observe that the change of basis matrix from the basis $\{ 1, x, x^2, ... \}$ to the basis $\{ p_0, p_1, p_2, ... \}$ is by construction triangular with $1$ s on the diagonal. Such a change of basis changes the Hankel matrices by a congruence $H_n \mapsto P_n^T H_n P_n$ where $P_n$ has determinant $1$ , and consequently does not affect the value of the Hankel determinants. We can therefore compute the Hankel determinants with respect to the basis of orthogonal polynomials. By construction, the Hankel matrices with respect to $\{ p_0, p_1, p_2, ... \}$ are diagonal:

$\displaystyle H_n = \left[ \begin{array}{ccccc} \mathbb{E}(p_0^2) & 0 & 0 & \hdots & 0 \\ 0 & \mathbb{E}(p_1^2) & 0 & \hdots & 0 \\ 0 & 0 & \mathbb{E}(p_2^2)& \hdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \hdots & \mathbb{E}(p_{n-1}^2) \end{array} \right]$ .

It follows that

$\displaystyle h_n = \prod_{i=0}^{n-1} \mathbb{E}(p_i^2) = \prod_{i=1}^{n-1} b_1 b_2 ... b_i$

as desired. $\Box$

Proof 2. We will give a combinatorial proof using the Lindström-Gessel-Viennot lemma. Consider the following locally finite directed acyclic graph $\tilde{G}$ : the vertices are the set of pairs $(x, y) \in \mathbb{Z}^2$ with $y \ge 0$ . The edges take the following forms:

edges $(x, i) \to (x + 1, i)$ with weights $a_i$ ,
edges $(x, y) \to (x + 1, y + 1)$ with weight $1$ , and
edges $(x, i + 1) \to (x + 1, i)$ with weights $b_{i+1}$ .

For a fixed positive integer $n$ , take the $n$ sources in the statement of the LGV lemma to be the vertices $(0, 0), (-1, 0), ... (-(n-1), 0)$ and take the $n$ sinks to be the vertices $(0, 0), (1, 0), ... (n-1, 0)$ . Then the paths from $(-i, 0)$ to $(j, 0)$ may be identified with closed walks of length $i + j$ on the weighted Motzkin graph $G$ (in the sense that there is a weight-preserving bijection between them), so the matrix appearing in the statement of the LGV lemma is precisely the Hankel matrix $H_n$ (with respect to the basis $\{ 1, x, x^2, ... \}$ ).

On the other hand, there is a unique non-intersecting $n$ -path in $\tilde{G}$ : the source $(-i, 0)$ is taken to the sink $(i, 0)$ by $i$ diagonal steps up and to the right, then $i$ diagonal steps down and to the right, and this is the unique possibility by induction on $i$ . This path has weight $b_1 b_2 ... b_i$ , from which the conclusion follows by the LGV lemma. $\Box$

Example. For the Wigner semicircular distribution with $R = 2$ , we know that $a_n = 0, b_n = 1$ for all $n$ , which gives $h_n = 1$ for all $n$ as desired.

Posted in math.CO, math.PR | Tagged Catalan numbers, generating functions, moments, walks on graphs | 6 Comments

6 Responses

on March 18, 2015 at 11:08 am | Reply Ehsan

Dear Qiaochu,

Thanks for sharing your valuable information. I have a question. Here what I understand was that we have a set of moments and then we use the Hankel determinants to determines a faithful state of the moments (let us say the moments are realizable if they grantee the Hankel determinants to be positive). Now my main question is that is there a reverse algorithm for this problem? What I mean is that we find a moments space where the hankel determinants are absolutely positive and then choose our moment set from that range? Thanks in advance for your valuable comment . Best, Ehsan
- on March 18, 2015 at 11:37 am | Reply Qiaochu Yuan
  
  Can you rephrase the question? I’m not sure I understand what you’re asking for.
  - on March 18, 2015 at 11:50 am | Reply Ehsan
    
    Faithfulness is equivalent to the condition that for every n the Hankel matrix
    
    \displaystyle H_n = \left[ \begin{array}{cccc} m_0 & m_1 & \hdots & m_{n-1} \\ m_1 & m_2 & \hdots & m_n \\ \vdots & \vdots & \ddots & \vdots \\ m_{n-1} & m_n & \hdots & m_{2n-2} \end{array} \right]
    
    with entries (H_n)_{i, j} = m_{i+j} is positive-definite. This is what I copy paste from your note.
    
    Let us say we work in the range between \left[ 0,1\right]. What I am asking is that is there any way that for example we find the root of the Hankel determinants. Then for example the positivity of the Hankel determinant be grantee between \left[0, x \right] where x is the root we found in the previous step and then define the moments which have the hankel determinants at that range?
    - on March 18, 2015 at 11:56 am | Reply Qiaochu Yuan
      
      No idea. The closest I can get you is that the positivity of the Hankel determinants is equivalent to the positivity of the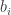 $b_i$ in the above notation, and these determine the moments, so you get a nice map whose image consists of faithful states.
on May 19, 2014 at 3:43 pm | Reply zemora

What’s the reference for this approach of Hankel determinants and Orthogonal Polynomials?
- on May 19, 2014 at 4:45 pm | Reply Qiaochu Yuan
  
  I don’t have a reference.

Comments RSS

	ZW on The double commutant theo…
	auto on More about the Schrödinger equ…
	Jaromir Kuben on Meditation on the Sylow theore…
	Qiaochu Yuan on Meditation on the Sylow theore…
	Qiaochu Yuan on Some remarks on the infinitude…

Annoying Precision

"A good stock of examples, as large as possible, is indispensable for a thorough understanding of any concept, and when I want to learn something new, I make it my first job to build one." – Paul Halmos