A less biased definition of a group

A first blog post on noncommutative rings »

A less biased definition of a group

January 16, 2012 by Qiaochu Yuan

Here’s what seems like a silly question: what’s the universal group? That is, what’s the universal example of a set $G$ together with maps

$\displaystyle e : 1 \to G, m : G \times G \to G, i : G \to G$

satisfying the identities

$m(e, x) = m(x, e) = x$ ,
$m(x, i(x)) = m(i(x), x) = e$ ,
$m(x, m(y, z)) = m(m(x, y), z)$ ?

A moment’s reflection shows that there isn’t such a group; the existence of e.g. the groups $\mathbb{Z}^S$ , where $S$ is an arbitrary set, shows that there exist groups of arbitrarily large cardinality, so no particular group can be universal.

However, it still seems like we can say things about the universal group, even though it doesn’t exist. That is, given a first-order statement in the language of groups, we can still give a sensible definition of what it means for that statement to be true in the universal group: it merely has to be true of all groups! Equivalently, by the completeness theorem for first-order logic, it merely has to be deducible from the group theory axioms. For example, it’s true in any group that

$\displaystyle x^n = e \Leftrightarrow (yxy^{-1})^n = e$

so this statement must be true in the universal group.

In fact, the universal group does exist: it’s just not a set! Namely, we can write down all of the objects $1 = G^0, G^1, G^2, G^3, ...$ together with all of the maps implied to exist by the existence of the structure maps $e, i, m$ , such as the map

$\displaystyle (xy z^{-1}, x^{-1}) : G^3 \to G^2$ ,

and together with all of the equalities between these maps implied by the group theory axioms. This data describes a category $T$ , in fact a category with finite products, that can be succinctly described as the free category with finite products on a group object. The object $G \in T$ is a group object which deserves the name “universal group” in the sense that, given any other category $M$ with finite products, the category of product-preserving functors $T \to M$ and natural transformations is equivalent to the category of group objects in $M$ .

The category $T$ is the Lawvere theory describing the theory of groups. It can be described more concretely as the opposite of the category whose objects are the free groups $F_n, n = 0, 1, 2, ...$ and whose morphisms are all group homomorphisms between these; indeed, the components of the universal maps $G^n \to G^m$ are just $m$ -tuples of elements of $F_n$ , which are the same thing as homomorphisms $F_m \to F_n$ , and it’s not hard to see that this identification respects composition.

Describing groups in this way has, to my mind, one major conceptual benefit over the standard definition: it emphasizes that the choice to present the theory of groups using a particular set of maps and axioms is just as arbitrary as the choice to present a group using a particular set of generators and relations. As long as one gets the same Lawvere theory $T$ in the end, one is still studying groups. For example, instead of using identity, multiplication, and inversion, we can use identity and the ternary map $xy^{-1} z : G^3 \to G$ together with the heap axioms.

Posted in math.CT, math.GR | Tagged Lawvere theories | 24 Comments

24 Responses

on April 12, 2019 at 9:32 pm | Reply Vandermonde

Incidentally, the axiom for inverse must be missing ‘= e’ in there since otherwise you can easily take i to be the identity (mapping) or constant e or similar.
on June 9, 2013 at 12:40 pm | Reply Operations and Lawvere theories | Annoying Precision

[…] Groups are in particular sets equipped with two operations: a binary operation (the group operation) and a unary operation (inverse) . Using these two operations, we can build up many other operations, such as the ternary operation , and the axioms governing groups become rules for deciding when two expressions describe the same operation (see, for example, this previous post). […]
on August 21, 2012 at 10:05 am | Reply Fourteenth Linkfest

[…] Yuan: A less biased definition of a group, A first blog post on noncommutative […]
on January 20, 2012 at 4:56 pm | Reply plm

I think I should say I am aware that I wrote alot of nonsense. In particular my proposed construction for a universal group in my proposed definition is wrong, and the definition is ill-thought.

I was trying to read a more about Lawvere theories, and actually check my beliefs carefully, before writing anything else. I guess I should just abstain from writing.

I apologize, I hope I did not bother you too much, Qiaochu, and other readers. And thank you again, this was very interesting, and still has me thinking.
on January 20, 2012 at 12:18 pm | Reply Franz

tiny comment;

did you mean to write

e: 1 -> G ?
- on January 20, 2012 at 12:37 pm | Reply Qiaochu Yuan
  
  Yes. I can’t tell if you’re offering a correction or if you’re confused about what this means. $1$ is the one-element set (more generally the identity object in a monoidal category) and $e : 1 \to G$ is the arrow that picks out the identity in $G$ .
  - on January 21, 2012 at 11:41 pm | Reply Franz
    
    Maybe I am unfamiliar with the practice, but I think calling a map – say e, mapping a one element set to G – only to then write e for the vale of the function at the point in the set – like in m(e,x) = … = x – is very confusing when you took the effort to be so formal writing all the group axioms ‘properly’.
    
    Sorry if this is obvious to everyone – if it is actually a mistake it would only be notational / conventional – but it certainly left me thinking if I was reading everything correctly.
    - on January 22, 2012 at 11:57 am | Reply Qiaochu Yuan
      
      It’s an abuse of notation. Such things are relatively common in mathematics. Have you never written $f$ for a function without naming its argument?
on January 17, 2012 at 9:46 am | Reply plm

I should have been more careful when talking of “union” of groups. A universal group should be a group containing any group as subgroup exactly once.

We should take unions of domains as long as the multiplications are compatible, and disjoint unions when they are not. We form all unions of maximal (under inclusion) sets of compatible group multiplications and take their domain as group-underlying set, and then take disjoint unions over all such distinct maximal sets, the domain is the disjoint union of domains obtained at the previous step.

Each group will belong to a single maximal set of multiplications. For each set underlying various groups we will have it as subgroup of the universal group once for each multiplication.

(Hopefully this is correct…)
- on January 17, 2012 at 10:47 am | Reply Qiaochu Yuan
  
  That constraint seems too strong to me. You only need to require that a universal group has a distinguished projection to any particular group and is universal with respect to this property. I am not convinced your construction makes sense.
- on January 18, 2012 at 5:29 am | Reply plm
  
  To confirm: your definition is equivalent to asking the universal group to be the direct sum of one representative for each isomorphism class of maximal groups -not contained in any other group?
  
  Then both possibilities, this or the direct sum of all groups, have merits I guess.
  
  One point I am not sure about is the condition “universal” with respect to having a projection to any group. I think asking for a unique morphism commuting with all the projections implies considering only maximal groups. But yes, I am not completely sure the constructions I propose are watertight.
  
  I understand you were not interested in actually constructing a universal group, I hope I will not bother too much.
  
  Another point: could you explicit “free monoidal category on a group object” in details? To confirm.
  
  Thank you.
  - on January 18, 2012 at 10:19 am | Reply Qiaochu Yuan
    
    No. I don’t know what you mean by “maximal group,” but perhaps an example where the universal example actually exists might clarify the situation. Consider the “universal cyclic group”: this is just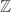 $\mathbb{Z}$ equipped with a distinguished map to itself and to the cyclic groups 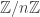$\mathbb{Z}/n\mathbb{Z}$ . It is not the direct sum of all the cyclic groups because this example is not minimal. “Universal” means that it satisfies a universal property, and so does “free.” “Free monoidal category on a group object” means, concretely, the following. You require that it has a group object $G$ and an identity $I = G^0$ for the tensor product, close it under tensor product, then add in all the morphisms given by the group operations, close them under tensor product, quotient by all relations implied by the group axioms, and do nothing else just as I said in the post.
- on January 19, 2012 at 3:17 am | Reply plm
  
  Thanks.
  
  Thinking about strict inclusions I badly overlooked that taking projections yields “many more” groups. Your example of Z is very nice. In part because it also shows that a universal object can easily be small.
  
  I was very wrong, the universal group in your definition is not a direct sum, and I wonder whether it exists in set theories with a universal set or class. I guess that it does.
  
  What I meant by maximal group is a group which is not properly contained in any other group as sets or classes, so these are proper classes -we can always direct-sum a small group with arbitrary ordinals as groups.
  
  Thanks for confirming the definition, the (perhaps unclear) point was that it should be parsed “free monoidal-category-on-a-group-object” and “group object” is with respect to tensor product, figuring what were the precise objects and morphisms of the category in which a free object on one generator should be taken.
  
  I still think we may wish to have a universal group similar to a universal set, where all groups must not only embed but be contained in, as sets. If we only require that they have a distinguished embedding (inject uniquely), the dual to your definition, I wonder how to construct the universal group.
  
  Finally I feel that if only for all the mistakes I have made here it was worth thinking of actual universal groups -I may be wrong :).
on January 17, 2012 at 4:07 am | Reply plm

Well those are not really “cyclic” groups, but cousins.
on January 17, 2012 at 4:04 am | Reply plm

Another basic way of seeing that the universal group is not a set: we take the large group of all ordinals with their inverses (doing something similar with cardinals looks nontrivial).

A related construction: supposing the axiom of choice, any set is well-orderable so in bijection with an ordinal \alpha (its order type), then we can pullback the group structure on \alpha obtained by quotienting the group-class of ordinals by the subgroup generated by \alpha. These are cyclic groups of order \alpha. Thus any set underlies a group.

Does the existence of a group structure on any set imply the axiom of choice?
- on January 17, 2012 at 11:12 am | Reply Zhen Lin
  
  In fact, yes: http://mathoverflow.net/questions/12973/does-every-non-empty-set-admit-a-group-structure-in-zf/12988#12988
  - on January 18, 2012 at 4:42 am | Reply plm
    
    Thank you. 🙂
on January 17, 2012 at 3:14 am | Reply plm

Nice, thanks Qiaochu. It would have been merciful to give more than the conceptual benefit as application of the idea (of a Lawvere theory). Because I know I will forget it again without some application in mind…

Since universes are often used in category theory, it is interesting to note that universal groups do exist (to construct them) in Grothendieck-Tarski, Feferman (reflection principles), NBG, etc. set theories. They are the set-theoretic unions of all groups (pairs (G,\cdot)) in a universal set/class -if I checked correctly, at least for the 3 examples betfore “etc.”.

I think there could be some more interesting set-theoretic observations to make about these concept and construction but am unable to find any.
- on January 17, 2012 at 10:57 am | Reply Qiaochu Yuan
  
  One application of the idea of Lawvere theories is that they are very general; for example, there is a Lawvere theory of Cartesian spaces which describes smooth algebras, a very general setting for differential geometry that allows infinitesimals.
on January 17, 2012 at 1:28 am | Reply Zhen Lin

Hm, I’m not sure your last comment is right. Every heap has the structure of a group, true, but I don’t think it’s canonical enough for the two Lawvere theories to be the same. (Are the categories of heaps and groups even equivalent?) Maybe you were thinking of the division-based axiomatisations of groups, e.g. here: http://www.cs.unm.edu/~mccune/projects/gtsax/
- on January 17, 2012 at 10:45 am | Reply Qiaochu Yuan
  
  A group is the same thing as a heap together with a distinguished element.
  - on January 17, 2012 at 11:24 am | Reply Zhen Lin
    
    But that’s precisely why I suspect their Lawvere theories are inequivalent! The Lawvere theory of groups contains an arrow 1 → X (or an arrow 0 → 1, if you prefer) corresponding to the unit element but I don’t see how any such arrow could be obtained in the Lawvere theory of heaps.
    
    Actually, there’s another problem: the theory of heaps specifies that a heap is non-empty, but that is a non-algebraic axiom. In particular this means there is no Lawvere theory of heaps. (If there are no constants in a Lawvere theory, then the empty set is a model of the theory.) The only way to make the inhabitation axiom into an algebraic axiom is to Skolemise and introduce a constant to the theory; but then per the usual conventions homomorphisms of this modified theory must preserve this constant. So we get the theory of pointed heaps… which is indeed the theory of groups, as you say.
    - on January 17, 2012 at 11:52 am | Reply Qiaochu Yuan
      
      Yes. Was I claiming otherwise?
  - on January 17, 2012 at 11:54 am | Reply Zhen Lin
    
    Ah, now I see. You wrote “identity and …”. What a difference two words make…

Comments RSS

	ZW on The double commutant theo…
	auto on More about the Schrödinger equ…
	Jaromir Kuben on Meditation on the Sylow theore…
	Qiaochu Yuan on Meditation on the Sylow theore…
	Qiaochu Yuan on Some remarks on the infinitude…

Annoying Precision

"A good stock of examples, as large as possible, is indispensable for a thorough understanding of any concept, and when I want to learn something new, I make it my first job to build one." – Paul Halmos