Let’s think more about what an abstract theory of unique factorization of primes has to look like. One fundamental property it has to satisfy is that factorizations should be finite. Another way of saying this is that the process of writing elements as products of other elements (up to units) should end in a finite set of irreducible elements at some point. This condition is clearly not satisfied by sufficiently “large” commutative rings such as , the ring of fractional polynomials.
Since we know we should think about ideals instead of numbers, let’s recast the problem in a different way: because we can write for any
, the ascending chain of ideals
never terminates. In any reasonable theory of factorization writing
and then comparing the ideals
, then repeating this process to obtain a chain of ideals
, should eventually stabilize at a prime. This leads to the following definition.
Definition: A commutative ring is Noetherian if every ascending chain of ideals stabilizes.
Akhil’s posts at Delta Epsilons here and here describe the basic properties of Noetherian rings well, including the proof of the following.
Hilbert’s Basis Theorem: If is a Noetherian ring, so is
.
Today we’ll discuss what the Noetherian condition means in terms of the topology of . The answer turns out to be quite nice.
Examples
The Noetherian condition is actually so strong that not every UFD satisfies it! For example, the ring of polynomials in countably many variables doesn’t satisfy the Noetherian condition because
doesn’t stabilize, but this ring is clearly a UFD because the factors of any given polynomial lie in a finitely-generated subring. But from a geometric perspective we don’t really care about such rings, since
contains
. From a practical perspective any question concerning finitely many elements of this ring actually happens in a Noetherian subring.
As we saw above, the Noetherian condition implies that every non-zero non-unit is a product of irreducibles, although this representation is not necessarily unique. It follows that a Noetherian integral domain is a UFD if and only if every irreducible element is prime.
The Noetherian condition is equivalent to the condition that every ideal of is finitely generated, so it follows that PIDs are Noetherian, hence
are Noetherian. Hilbert’s basis theorem together with a few other basic facts then tell us that any finitely-generated algebra over a Noetherian ring is Noetherian, so anything we want to do with polynomial rings or number rings will stay in the Noetherian regime.
Compactness
Remember that when we wanted to characterize the maximal ideals of the ring of continuous functions on a compact Hausdorff space, we needed the compactness condition to take an ideal
not contained in the ideals
and extract finitely many elements
of it. The Noetherian condition automatically lets us do this, so it’s reasonable to suppose that the Noetherian condition is equivalent to a kind of compactness. In fact, more is true.
Proposition: If a commutative ring is Noetherian, then every subset of
is compact in the Zariski topology, i.e.
is hereditarily compact, also known as Noetherian.
Proof. Let . It is a general topological fact that to show that every open cover of a space has a finite subcover it suffices to do so for open covers by a basis of the topology, which here is given by the sets
. So let
be such an open covering of
. The ideal
generated by all the
is finitely generated, say by
. For any point
there is some
such that
, so the same must be true for the generators
, and this is equivalent to
being a finite subcover.
Unfortunately, the converse is false. For example, let . The “evaluation” homomorphism sending a power series to its constant term has kernel the maximal ideal
, and since any element of
is invertible in
, it follows that
is the unique maximal ideal, so
consists of a single point, i.e.
is a local ring. But the ascending chain of ideals
does not stabilize. (I believe replacing
with
, the prime spectrum, fixes this equivalence, but we won’t worry too much about the prime spectrum for now.)
Corollary: If is Noetherian and
is Hausdorff, then
is finite.
Zorn’s lemma
I sort of glossed over why we know that is non-empty. To prove this we need to know that every ideal of
is contained in a maximal ideal. For general rings with unity this is a consequence of Zorn’s lemma, which I am reticent to apply since it is equivalent to the axiom of choice. However, for Noetherian rings one can get by with the axiom of countable choice, which is yet another reason to like Noetherian rings.
Next time we’ll see how the Noetherian condition allows us to decompose a variety into components.
I’ve always been under the impression that even Spec doesn’t know enough when the ring is not Noetherian — for example, the power series ring k[[x]] has a unique non-zero prime ideal (any power-series with non-zero constant term is invertible, so the ideals are (1), (x), (x^2), …, 0), but geometrically the corresponding scheme _should_ be (the generic point and) a very large fuzzy point.
Similarly, for any n, I think that Spec(k[x]/x^n) is a single point, right? Again any polynomial that starts at 1 is invertible, so the ideals are (1), (x), …, (x^{n-1}). So the set-valued Spec (or topological-space-valued) really isn’t good enough; you need Spec to take values in locally-ringed spaces. And this is in the Noetherian regime — there are finitely many ideals.
But I’m not much of an algebraic geometer.
By the way, I’ve been very much enjoying the recent series of posts.
Are you planning on talking about commutative C* algebras? I really don’t know whether I believe that the correct algebraic data to attach to a (locally compact Hausdorff) topological space is the ring of all continuous functions or the ring of functions that vanish at infinity. The former seems better suited for an analogy with algebraic spaces; the later provides easier analytic tools.
“I’ve always been under the impression that even Spec doesn’t know enough when the ring is not Noetherian”
Your first example is noetherian though–am I misunderstanding you?
I agree that the structure sheaf clears up these issues, but I’m trying to stay away from machinery for now.
I don’t really know enough functional analysis to say anything meaningful about -algebras, so probably not; my goal for the time being is just to understand Dedekind domains thoroughly.
-algebras, so probably not; my goal for the time being is just to understand Dedekind domains thoroughly.
“(I believe replacing with , the prime spectrum, fixes this equivalence, but we won’t worry too much about the prime spectrum for now.)”
One implication is true.
If is a valuation ring whose value group is
is a valuation ring whose value group is 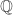 , then
, then  has only one prime ideal but is not noetherian.
has only one prime ideal but is not noetherian.
I learned this by googling the question and finding these notes. But I disagree with the author’s assertion that this is because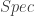 only gives information about prime ideals; knowing that the primes are finitely generated is enough to conclude that a ring is noetherian.
only gives information about prime ideals; knowing that the primes are finitely generated is enough to conclude that a ring is noetherian.
Minor correction – valuation rings have two prime ideals, the unique maximal ideal and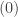 .
.
What you can show is that being Noetherian implies that every ascending chain of radical ideals terminates (and if
being Noetherian implies that every ascending chain of radical ideals terminates (and if  is Jacobson it’s enough to show this for
is Jacobson it’s enough to show this for  ). The problem here is that one may have a chain of, say, primary ideals, all of which have the same radical, that does not.
). The problem here is that one may have a chain of, say, primary ideals, all of which have the same radical, that does not.
Hm, yes, you’re right about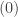 .
.
But I think you can have more than two prime ideals if the value group is large enough (e.g.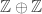 with the lexicographic order—then take the ideal corresponding to elements with valuations
with the lexicographic order—then take the ideal corresponding to elements with valuations  for
for 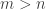 ; I think this is done systematically in Zariski-Samuels).
; I think this is done systematically in Zariski-Samuels).
What I said in my previous comment is false; however, two non-maximal nonzero prime ideals in that valuation ring should arise from elements with valuations with, respectively,
with, respectively, 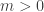 , and
, and 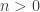 .
.