Standard Young tableaux and Robinson-Schensted-Knuth

« IMO 2009 and proof systems

Standard Young tableaux and Robinson-Schensted-Knuth

July 22, 2009 by Qiaochu Yuan

Earlier I mentioned that the theory of Young tableaux is the source of one of my favorite proofs. Today I’d like to present, again from the theory of Young tableaux, one of my favorite pairs of proofs.

A standard Young tableau is a chain in Young’s lattice; equivalently, it is a sequence of Young diagrams, each of which has exactly one more box than the previous. One can succinctly write down such a chain by taking the last Young diagram in the chain and recording the “path” traced out by the rest of the chain: write down a 1 in the box corresponding to the first Young diagram, a 2 in the box added by the next Young diagram, and so forth. In other words, a standard Young tableau is a Young tableau filled with positive integers $1, 2, ... n$ which is strictly increasing across rows and columns.

Given a Young diagram $\lambda$ , let $f^{\lambda}$ denote the number of standard Young tableaux of shape $\lambda$ ; equivalently, one can define $L(\lambda)$ to be the poset of Young diagrams fitting inside $\lambda$ , and then $f^{\lambda}$ is equal to the number of maximal chains of $L(\lambda)$ .

Finally, one last bit of notation. If $\lambda$ is a Young diagram for a partition of $n$ , we will write either $|\lambda| = n$ or $\lambda \vdash n$ . Then we have the following beautiful result.

Theorem: $\displaystyle \sum_{\lambda \vdash n} (f^{\lambda})^2 = n!$ .

The representation-theoretic proof, which I believe is the method by which the theorem was first discovered, is this: every Young diagram $\lambda$ has an associated Specht module that defines an irreducible representation of $S_n$ , and the dimension of this representation turns out to be precisely $f^{\lambda}$ ; in fact it is possible to write down the basis explicitly. Since the number of conjugacy classes in $S_n$ is precisely the number of partitions of $n$ , these are all the irreducible representations. For example, the single row diagram corresponds to the trivial representation, while the single column diagram corresponds to the sign representation. In any case, standard results in representation theory then guarantee that for a finite group $G$ with irreducible representations $V_1, ... V_k$ , it is true that

$\displaystyle |G| = \sum_{i=1}^{k} (\dim V_i)^2$

and then the result follows as a corollary.

In the spirit of bijective combinatorics, however, the appropriate combinatorial interpretation of this identity is that there is a bijection between permutations and pairs of standard Young tableaux of the same shape. The interesting question is whether this bijection can be concisely described.

This is the content of the second proof: exactly such an explicit bijection is provided by the Robinson-Schensted-(Knuth) algorithm. Stanley provides a good explanation of the algorithm as well as a proof of a stronger result concerning so-called Hasse walks in Young’s lattice using operator methods, but it is not so much the details of the algorithm I want to talk about so much as its existence.

The fact that there can exist two proofs of the same result that are so different is fascinating to me. The network of ideas in this area bring together combinatorics, representation theory, invariant theory and symmetric function theory, and via Schur-Weyl duality relate to the representations of the linear groups as well, an important subject to physics and other branches of mathematics that one would think to be far removed from combinatorics.

Even without knowing all this, there are many questions raised by the existence of these two proofs. For example, how much information about a representation can be read off from the corresponding Young diagram? A lot, as it turns out: for example, if a representation of $S_n$ is given by a Young diagram $\lambda$ , then its induced representation in $S_{n+1}$ is given by a direct sum over the representations corresponding to Young diagrams obtained by adding one box to $\lambda$ , i.e. all elements covering $\lambda$ in Young’s lattice. Similarly the restricted representation in $S_{n-1}$ is a direct sum over the representations corresponding to Young diagrams obtained by removing a box from $\lambda$ . For a very readable introduction to these ideas, consult Yufei Zhao’s article in the Harvard College Mathematics Review.

Perhaps the only downside of the subject is that as it’s usually presented the relationship between Young tableaux and representations of the symmetric group is not deduced, but rather claimed (at least I have never seen anyone explain in intuitive terms why this should be.) A purely deductive approach would presumably carry over to other Coxeter groups as well, and indeed this seems to be the goal of this paper by Okounkov and Vershik.

Incidentally, it’s only very recently that I’ve come to learn that most research doesn’t consist of constructing new theories and solving open problems; a lot of it consists of compressing old theories into more manageable chunks or solving old problems in new, shorter ways. It seems to me that academic culture tends to undervalue this to some extent.

8 Responses

on October 20, 2012 at 1:44 pm | Reply Jacobi-Trudi identities « caozhu

[…] right we are at Qiaochu’s post Standard Young tableaux and Robinson-Schensted-Knuth. A Young tableau is a chain in Young’s lattice which can be represented in a augumenting way. […]
on July 23, 2009 at 2:11 pm | Reply Akhil Mathew

Thanks for the reference.

I looked at Sagan’s book a few weeks back to learn about the symmetric group but failed to finish much of it. The Novelli et al paper has an interesting proof, which may actually be in Sagan, although I didn’t quite reach it.
on July 23, 2009 at 11:56 am | Reply Steven Sam

Also, for “naturality” of Young tableaux popping in representation theory, you might find Kashiwara’s article on crystal bases (http://www.kurims.kyoto-u.ac.jp/~kenkyubu/kashiwara/on-crystal.pdf) useful (especially section 4 and 5).

Given the crystal graph for the standard representation of $U_q(\mathfrak{gl}_n)$ , tensor it with itself a bunch of times and find the connected components of the resulting crystal graph. Then elements of these components are in bijection (in a not so bad way) with semistandard Young tableaux, but whether or not this realization is natural enough depends on your taste.

And then we just specialize to q=1 to get information about usual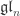 $\mathfrak{gl}_n$ .
on July 23, 2009 at 5:47 am | Reply Akhil Mathew

“The representation-theoretic proof, which I believe is the method by which the theorem was first discovered, is this: every Young diagram \lambda has an associated Specht module that defines an irreducible representation of S_n, and the dimension of this representation turns out to be precisely f^{\lambda}; in fact it is possible to write down the basis explicitly. ”

Therefore, $f^{\lambda}$ is the same as the number given by the hook length formula. This is interesting. Is there a direct way to prove this?
- on July 23, 2009 at 10:13 am | Reply Harrison
  
  I believe that’s essentially how the original proof proceeded (i.e., showing that the hook-length formula computed the dimension of the irreducible representation corresponding to $\gamma$ ), although I could easily be mistaken.
  
  There’s a lot of interesting stuff on this in Sagan’s book, and apparently Macdonald’s book on symmetric functions is also really good.
- on July 23, 2009 at 10:13 am | Reply Harrison
  
  And, of course, I was reading the post upside-down and in a mirror and confused $\gamma$ with $lambda$ . 🙂
- on July 23, 2009 at 10:54 am | Reply Qiaochu Yuan
  
  There’s a direct bijective proof and some references here. What I always thought was interesting is that there’s a naive probabilistic proof that makes perfect sense, except that it assumes certain events are independent when they’re clearly not, so it doesn’t work.
  - on July 23, 2009 at 11:35 am | Reply Steven Sam
    
    Here’s a probabilistic proof of the hook-length formula. I like it very much:
    http://dx.doi.org/10.1016/0001-8708(79)90023-9

Comments RSS

	waltonmath on Maximum entropy from Bayes…
	Richard Stanley on Finite index subgroups of the…
	Dean on The adjoint functor theorem fo…
	Qiaochu Yuan on The adjoint functor theorem fo…
	Dean on The adjoint functor theorem fo…

Annoying Precision

"A good stock of examples, as large as possible, is indispensable for a thorough understanding of any concept, and when I want to learn something new, I make it my first job to build one." – Paul Halmos