John Ewing wrote up a nice collection of quotes from Paul Halmos for the Notices of the AMS; let’s meditate on his words.
For example:
The best notation is no notation; whenever possible to avoid the use of a complicated alphabetic apparatus, avoid it. A good attitude to the preparation of written mathematical exposition is to pretend that it is spoken. Pretend that you are explaining the subject to a friend on a long walk in the woods, with no paper available; fall back on symbolism only when it is really necessary.
I’d have to agree. I see this as one of the strongest aspects of, for example, Terence Tao’s expository style. His latest post on relativization is a perfect example; Tao is a master at recognizing when technical details would obscure his exposition and when they are necessary. A related point:
To explain something you must know not only what to put in, but also what to leave out; you must know when to tell the whole truth and when to get the right idea across by telling a little white fib.
This seems to be a much more common practice in science exposition; expositors of physics are never telling you all the details of, for example, the mathematics of quantum mechanics. Nearly everything is a convenient analogy. Unfortunately, I think this triggers a backlash on the part of mathematicians who are concerned with communicating “the whole truth.” Again, Terence Tao does this very well.
I have taught courses whose entire content was problems solved by students (and then presented to the class). The number of theorems that the students in such a course were exposed to was approximately half the number that they could have been exposed to in a series of lectures. In a problem course, however, exposure means the acquiring of an intelligent questioning attitude and of some techniques for plugging the leaks that proofs are likely to spring; in a lecture course, exposure sometimes means not much more than learning the name of a theorem, being intimidated by its complicated proof, and worrying about whether it would appear on the examination.
This is an interesting point. I think trying to understand undergraduate mathematics without experience with problem solving can be problematic, although I can’t speak from personal experience. It seems to me that you don’t really understand or care about a theorem until you’ve used it to solve at least one problem you were aware of before you learned the theorem. For example, I feel uncomfortable with most of the material I learned in my functional analysis class last semester because I have yet to solve an independently interesting problem using, for example, the Hahn-Banach theorem. Probably the only idea I really retained from that class is the use of well-behaved dense subspaces, since density arguments have a wide range of applicability.
Mathematics – this may surprise or shock you some – is never deductive in its creation. The mathematician at work makes vague guesses, visualizes broad generalizations, and jumps to unwarranted conclusions. He arranges and rearranges his ideas, and he becomes convinced of their truth long before he can write down a logical proof.
This statement appears as part of a longer passage explaining mathematics to non-mathematicians, and I think this aspect of mathematics deserves to be emphasized in general. To be convinced that this is the case one only has to read the comments at the n-category cafe, but I imagine most people’s concept of what mathematicians do is much duller.
First of all, I assumed you meant “problem-solving” in the sense of typical contest math, not in the sense of Gowers’ article. I don’t object to either, since I did a research project a couple of years back that would surely qualify as “problem-solving” in Gowers’ language and enjoyed myself thoroughly; I have a strong interest in analysis. I also don’t mind contest problems per se, at least in moderation, although I seem to lack the quick mind necessary for success here.
My critique was the question: How is it possible to do what you are asking? After looking at a couple of Putnam exams now, I think I see your point there, although I still don’t know whether you can get AIME problems in complex analysis courses, or Pavel Etingof’s famous representation theory course.
To do this would make the course much more difficult than it is now, since Putnam problems are (presumably) harder than typically assigned exercises, no? Unless you think the problems should be worked out during the class, by the instructor?
Then again, since your definition of problem-solving is apparently more expansive than what I initially thought, perhaps I should ask for examples of what you are looking for to improve the undergraduate curriculum? Should someone discussing Fourier transforms give examples from the IMO as motivation?
It may also be possible (though I don’t have any experience in MIT undergraduate coursework) to do what someone like Rudin does really well in his books: develop the basic definitions, theorems, and proofs, and then spend some time using them to prove nontrivial results in other areas. For instance, he discussed approximation-theory proofs like Runge’s theorem in the context of the Hahn-Banach theorem, which is probably the main reason I still remember it now. Or Fourier series in the context of Hilbert spaces, or the divergence of Fourier series in the context of the Banach-Steinhaus theorem. This puts the results in a clear context and shows their applications, although I don’t know whether it classifies as problem-solving.
I don’t know if I’m necessarily qualified to come up with a workable curriculum on the spot, but here are some ideas. A problem-solving approach to complex analysis might focus more strongly on its applications to combinatorics and number theory, since in practice one of the most important uses of complex analysis is to extract asymptotics and it would be good if this were emphasized. Many Olympiad problems take the form “show that this polynomial is irreducible” and one neat way to do this is to use tricks such as Rouche’s theorem to show that the polynomial can only have a certain number of roots outside of the unit circle.
I also think you misinterpreted what Halmos is suggesting: for him the problems replace the course. I think this is a great idea for certain subjects (say, number theory) and not so great for others (say, representation theory), but even there I think some compromise is possible. For example, one could focus on the applications to physics, but I’m not qualified to discuss those in any detail.
Anyway, it’s not as if all courses should be done this way. I just think even a single problem-based course would do most math majors a world of good.
“I think a problem-oriented approach to undergraduate mathematics helps reveal connections between different branches of mathematics. Suppose you encounter an Olympiad problem and solve it in two ways, using tools from different branches of mathematics. That’s your cue to attempt to relate the different tools you just used. This has happened to me personally several times and I learn a great deal each time.”
But how do you make abstract algebra, category theory, algebraic geometry, complex analysis, or the theory of Lie algebras look like a USAMO problem? An elementary problem in algebraic geometry might be, for instance, to show that locally free sheaves of rank one are invertible (I am copying Hartshorne here), which does not (as far as I know) have an easy analog in terms of a math competition problem.
I think that emphasizing multiple proofs is a good idea, which certainly helps me gain a better understanding (hence I like to read multiple sources whenever possible). The question is whether any one of them looks like contest math.
“Homothety and spiral symmetry, both of which are important tools in elementary Euclidean geometry, are also special cases of conformal maps, which you cannot deny are extremely important to complex analysis. So I would venture to guess that a thorough mastery of these tools can only help a beginning complex analyst.”
But homotheties are just multiplications and admit an easy visualization (and an algebraic description). Do these frequently occur in geometry contest problems? I don’t know anything about spiral symmetries, so I can’t comment here.
A book like Rudin, for instance, develops complex analysis without any geometry and no pictures.
Some points to clear up: first, “experience with problem solving” isn’t limited to the AMC. For example, it was either Doron Zeilberger or Gil Kalai (I can’t remember which) who remarked that a certain Israeli math journal that posed very interesting problems on a regular basis was at least partly responsible for the prowess of the Israeli mathematicians of that generation.
Second, we seem to be heading into problem-solving vs. theory-building territory, so I’ll take advantage of that language: I think the standard structure of a class (definitions, theorems, proofs) is heavily biased towards theory-building and that a healthy dose of problem-solving is a good way to have a balanced perspective on mathematics.
As for your concrete question, abstract algebra can be very useful in Olympiad math. For example, one way to solve IMO 2008 #5 boils down to the discrete Fourier transform, i.e. representations of finite abelian groups. The best example of “algebraic geometry” that comes to mind at the moment is AIME 2008 #13‘s use of the fact that two cubic curves that share eight points must share nine, which is related to Bezout’s theorem. But even most math majors don’t encounter algebraic geometry until graduate school, so this is sort of an unfair question. Abstract algebra and complex analysis also show up all the time on the Putnam exams.
The real criticism you seem to be hinting at is that you find contest math boring, which is fine; it just means you’re more of a Grothendieck than an Erdos. But all the little Grothendiecks out there are already in an educational environment suited to their development, whereas it seems to me that the little Erdoses get shortchanged.
Ok, so in that case I think I know some undergraduate mathematics, although I have very litte experience (and am not very good at) AMC-type problem-solving competitions. Why do you think the latter helps with the former? For instance, to do well in the USAMO, you have to be very comfortable with obscure areas of Euclidean geometry, but that’s not much help in, say, complex analysis or representation theory.
That said, I myself find it useful to learn things first in a concrete setting and then move to a more abstract one; I did not understand what a category was until I had seen several examples, and am only now starting to understand the motivation from topology, algebraic geometry, etc.
But I definitely found the structure theorem for PIDs helpful; I never understood Jordan normal form without it, and it seems much more natural to use it than to give ad hoc proofs.
Incidentally I had a professor who, when asked about advice on number theory, said: “First learn number theory, then algebra, then number theory again.”
Certainly there are many ways to gain mathematical maturity. Let me clarify what I was trying to say with a less extreme statement: I think a problem-oriented approach to undergraduate mathematics helps reveal connections between different branches of mathematics. Suppose you encounter an Olympiad problem and solve it in two ways, using tools from different branches of mathematics. That’s your cue to attempt to relate the different tools you just used. This has happened to me personally several times and I learn a great deal each time.
And sometimes even one solution is revealing: for example, Jacob Steinhardt’s solution to USAMO 2008 #6 is a great example of the use of linear algebra in combinatorics, a subject Tim Gowers has also discussed. I think people would be more interested in linear algebra if they were exposed to its applications in the less algebraic branches of mathematics.
Euclidean geometry is an interesting example. I think it is very interesting to classify geometry problems based on the bare minimum of the properties of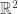 they require: some problems are essentially projective, others conformal, and so forth. Homothety and spiral symmetry, both of which are important tools in elementary Euclidean geometry, are also special cases of conformal maps, which you cannot deny are extremely important to complex analysis. So I would venture to guess that a thorough mastery of these tools can only help a beginning complex analyst. (I could also claim that groups related to the Euclidean group are in some sense the motivating case for studying the representation theory of Lie groups, but I think I’d be pushing it.)
they require: some problems are essentially projective, others conformal, and so forth. Homothety and spiral symmetry, both of which are important tools in elementary Euclidean geometry, are also special cases of conformal maps, which you cannot deny are extremely important to complex analysis. So I would venture to guess that a thorough mastery of these tools can only help a beginning complex analyst. (I could also claim that groups related to the Euclidean group are in some sense the motivating case for studying the representation theory of Lie groups, but I think I’d be pushing it.)
“This is an interesting point. I think trying to understand undergraduate mathematics without experience with problem solving can be problematic, although I can’t speak from personal experience.”
Just curious- what do you mean by undergraduate mathematics?
I guess I actually meant “mathematics beyond that required of a non-major.” For example, someone I know who took an abstract algebra class expressed disdain at structure theorems because he preferred results that would help him compute and solve problems. The structure theorem for finitely generated modules over a PID can be used to deduce the Chinese Remainder Theorem, partial fraction decomposition, Lagrange interpolation, the existence of Jordan normal form… all of which are extremely useful for computations and problem-solving.