IMO medalist Iurie Boreico has an article in an issue of the Harvard College Mathematics Review about his favorite problem:
Let
be distinct squarefree integers. Show that if
are not all zero, then the sum
is nonzero.
In other words, the problem is to show that there are no “unexpected” linear relationships between the fractions . This is one of those nice problems that justifies an intuition without being amenable to the obvious attacks. Iurie gives several ingenious Olympiad-style arguments, i.e. arguments that don’t require much machinery, including a clearly motivated argument that serves as a good way to motivate the definition of a Galois group.
Today I want to share a different argument that generalizes a simple argument for special cases, but it has the unfortunate property that in full generality it is severe overkill.
First of all, it may not be clear that the problem statement implies that numbers such as are irrational; it only implies that they are non-integer. However, it’s known that the sum of algebraic integers is again an algebraic integer, and it is also known, via the rational root theorem, that the only rational algebraic integers are the integers. (Even if you aren’t familiar with the proofs of these results, I would like to stress that they are straightforward compared to the results we’ll be citing by the end of this post!) So the problem statement does involve showing that a large class of sums that we expect to be irrational are in fact irrational.
The very simplest special case of this problem requires showing that is irrational for
a square-free integer. This is a well-known classical problem in number theory dating back to the Greeks; one can argue by contradiction and prime factorization, from the rational root theorem, or from the fact that
has a periodic continued fraction. The first argument is elementary, the first and second generalize readily to
powers, but the third is my favorite; it is the basis of a certain proof you may have seen of the irrationality of
which disguises a proof of the identity
.
There is a fourth argument I would like to present, and it may seem silly at first: cannot be an integer because
is not a quadratic residue
.
Why is this sufficient? Suppose for some integer
. Then
, which implies that
, but checking
we readily see that this can’t occur; contradiction.
This is the seed of an important idea, which can be stated roughly as follows.
Important idea: Certain statements have the property that if they are true locally (i.e. modulo a prime), then they are true for the integers.
More precisely, we need the following result.
Proposition: Let be a monic polynomial with integer coefficients. If
is irreducible over
, then
is irreducible over
. (The reverse implication does not hold in general.)
In other words, if an algebraic integer is “locally irrational,” then it must be irrational. This is the first conceptual ingredient of our proof.
Here’s the second. Suppose I want to prove that is irrational. I want to reduce this to a statement about the irrationality of a single square root, since I already know how to deal with that by finding a suitable prime (under the assumption that such a prime exists). So here’s the trick: find a prime such that
is a quadratic residue, but
isn’t!
Here’s how this works with . Suppose
for some integer
. Since
, this is equivalent to
, but again checking
(or using Euler’s criterion) we can readily verify that
isn’t a quadratic residue
; contradiction.
Problems of this sort were often given on my abstract algebra problem sets before we covered Galois theory. I think the intended solution was either to square (which, as Iurie mentions, stops working for sums of more than four square roots) or to show that the minimal polynomial is irreducible. But one of the easiest ways to show that a polynomial is irreducible is to show that it’s irreducible modulo a prime – this is the motivation behind Eisenstein’s criterion – and so we are led back to this idea anyway, which we can implement without actually computing the minimal polynomial.
On another problem set we were asked to show that was not an element of
; since
is an algebraic integer, this is equivalent to showing that
isn’t of the form
for integers
. (Well, up to the small problem that I don’t have a good proof that the ring of integers in
is
, but for now I’ll take this as given.) The trick is to find a prime relative to which
is a cubic residue, but
isn’t. It turns out that
is such a prime, since
but
(this is the cubic generalization of Euler’s criterion). So this “find a prime” method works well for specific cases, but I haven’t described a general way to find the magical primes we need. The intuition we want here is that numbers that are unrelated multiplicatively behave independently modulo various primes. So we need to prove a statement like the following.
Conjecture: Let be distinct primes. Then there exists an arbitrarily large prime
relative to which
are quadratic residues, but
isn’t.
First let’s verify that this conjecture implies the desired result. Given a sum of integer combinations of distinct squarefree integers that might be equal to zero, we’re going to induct on the number of distinct primes
that appears in
. Clearly the original problem statement is satisfied for
. Now, any such sum can be written as a polynomial in some set
of square roots of primes. The monomials of this polynomial are squarefree, i.e. the polynomial is linear in each variable, so we can write
where are integer linear combinations of products of distinct elements of the set
and
is nonzero by the inductive hypothesis. Actually, the inductive hypothesis gives us something stronger, which is that all of the conjugates of
are also nonzero, hence the minimal polynomial of
has nonzero constant term, i.e. the norm of
is nonzero.
This is important. Now we pick a prime satisfying the hypotheses of the conjecture such that
does not divide this constant term (which is why we need
to be arbitrarily large). Then any “reduction” of
is still nonzero and
is a contradiction.
The hard part, of course, is proving the conjecture. I see no way to do it that doesn’t require the following two tools: quadratic reciprocity and Dirichlet’s theorem. Quadratic reciprocity is a gem of number theory; it not only validates the assumption that numbers behave independently modulo primes, but it makes the astonishing claim that whether a prime is a quadratic residue
depends only on the residue class of
. Dirichlet’s theorem is another validation of intuition: it lets us find arbitrarily large primes in arbitrary residue classes exactly like the ones we need for quadratic reciprocity.
Now for every there exists a residue class
such that
is a quadratic residue relative to primes in this residue class by quadratic reciprocity. There also exists a residue class
such that
is not a quadratic residue relative to primes in this residue class, again by quadratic reciprocity. If we choose all the
to be congruent
(and we can always do this), then by CRT there exists a residue class
such that
are quadratic residues relative to primes in this residue class but
isn’t. By Dirichlet’s theorem, this residue class contains arbitrarily large primes, and we’re done.
If that seemed like more work than was necessary to solve this problem, it probably was. But I think this argument is a good demonstration of the local perspective in number theory. It also suggests that it would be useful to understand higher-order reciprocity laws in order to generalize the proof to higher powers, but this leads into waters so deep they justify themselves as of independent interest.
[…] This equation can only hold if all sqrt are natural numbers, up to a common factor $k$ by this theorem […]
Here is an attempted proof, somewhat along your lines, that the sum S of a finite set of signed square roots of distinct squarefree integers can never equal an integer. Multiply (x-S) over all choices of the signs within S. Result is a monic polynomial(x) with all-integer coefficients. If this polynomial can be proven to be irreducible, or merely proven to have no integer-valued roots x, then we are done. Suppose P is a prime such that the polynomial has no roots mod P. Then again we are done. Now claim if P is such that none of the square roots exist mod P (i.e. their arguments all are nonresidues mod P) then the polynomial has no roots mod P. An infinity of such primes P must exist by combining (a) quadratic reciprocity, (b) Chinese remaindering, (c) Dirichlet theorem on primes in arithmetic progressions.
Was that proof valid? I think it all is ok except I am worried about the “then” clause inside the sentence “Now…”.
Hmm, actually, instead of the prime P that I had in mind (in my comment earlier today) the prime you construct, with respect to which all the square roots exist except one — that prime really does work in my proof. Which then is seen to be a somewhat disguised version of your proof.
This is an interesting post. A naïve question: what is the minimal formality required to justify the localization? I believe your argument is if the equations x^2=2, y^2=3, x+y=k can be solved in a finite extension of the rationals, then they can be solved in a finite extension of F_7. Did I capture this right?
The argument is more specifically that if they can be solved in a finite extension of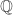 , then they can be solved in the ring of integers of that finite extension, and so they can be solved in the ring of integers of that finite extension
, then they can be solved in the ring of integers of that finite extension, and so they can be solved in the ring of integers of that finite extension 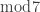 .
.
[…] Qiaochu Yuan writes about Kraft’s inequality for prefix codes and the probabilistic method, and also on linear relationships between square roots. […]
[…] Comments Non-update « P… on Exceptional structuresAhwing on Square roots have no unexpecte…skipper hartley on Aboutiura on Square roots have no unexpecte…Qiaochu Yuan on […]
What a coincidence! I made up this problem:
Given any n tuple of positive integers {a_i} find k such that {(a_i^k)+1} all have a common factor.
and I solved it with that conjecture in your post. I had the exact same proof for that conjecture as well. I really like this post of yours by the way.
Very nice proof, I like it very much. If i had known it, i would have definitely put it in my expository article. I can think of another “find a prime” application in the proof of the Minkowski-Hasse Theorem (special cases for forms of order 4). And then you have some ISL problems I think.. but you usually hit the Dirichlet theorem.
The start of a proof that the ring of integers in![Z[\sqrt[3]{2}]](https://s0.wp.com/latex.php?latex=Z%5B%5Csqrt%5B3%5D%7B2%7D%5D&bg=ffffff&fg=333333&s=0&c=20201002) is as claimed:
is as claimed:
Notice that the trace of an algebraic integer is an algebraic integer. A quick computation shows that![tr(a+b \sqrt[3]{2} + c \sqrt[3]{4})=3a](https://s0.wp.com/latex.php?latex=tr%28a%2Bb+%5Csqrt%5B3%5D%7B2%7D+%2B+c+%5Csqrt%5B3%5D%7B4%7D%29%3D3a&bg=ffffff&fg=333333&s=0&c=20201002) . So, if
. So, if ![z := a+b \sqrt[2]{2} + c \sqrt[3]{4}](https://s0.wp.com/latex.php?latex=z+%3A%3D+a%2Bb+%5Csqrt%5B2%5D%7B2%7D+%2B+c+%5Csqrt%5B3%5D%7B4%7D&bg=ffffff&fg=333333&s=0&c=20201002) is an algebraic integer, then
is an algebraic integer, then  ,
, ![tr(\sqrt[3]{2} z)=6b](https://s0.wp.com/latex.php?latex=tr%28%5Csqrt%5B3%5D%7B2%7D+z%29%3D6b&bg=ffffff&fg=333333&s=0&c=20201002) and
and ![tr(\sqrt[3]{4} z)=6c](https://s0.wp.com/latex.php?latex=tr%28%5Csqrt%5B3%5D%7B4%7D+z%29%3D6c&bg=ffffff&fg=333333&s=0&c=20201002) are all integers.
are all integers.
Now, you just need to do local analyses at the primes 2 and 3. I have reasonably elegant ways of doing these, but nothing super-slick.
hey, the proof of the first problem is pretty easy from elementary vector space arguments, right ?
… anyway it’s nice to see your blog, i’m also a student of math 🙂
I’m not sure what you mean. Could you elaborate? Showing that square roots are linearly independent over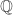 can’t really be done without appealing to the specific number-theoretic properties in play in some form or other.
can’t really be done without appealing to the specific number-theoretic properties in play in some form or other.